Post

[코딩테스트 합격자 되기 스터디] 9주차 - 동적 계획법 (9.1 ~ 9.7)

Posted
By Je Hun Lim 11 min read

코딩테스트 합격자 되기 스터디 9주차

강의 보기 -> 해당되는 부분 책 다시 읽기 -> 블로그 정리
강의는 C++로 되어 있지만 개념적인 내용이라 언어 상관 없이 보고 코드는 각 언어에 맞게 바꾸면 된다.

참고 강의 및 책

인프런 : 코딩테스트 합격자 되기 파이썬, C+_+ 저자님 인프런 강의 링크
Youtube : 코딩테스트 합격자 되기 파이썬, C+_+ 저자님 Youtube 링크
종이책 : 코딩테스트 합격자 되기 파이썬 편
종이책 : 코딩테스트 합격자 되기 C++ 편
종이책 : 코딩테스트 합격자 되기 자바스크립트 편
종이책 : 코딩테스트 합격자 되기 자바 편

동적 계획법

  • 복잡한 문제를 단순한 하위 문제로 나눠서 접근하는 방법
  • 중복 계산을 줄이기 위해, 이전에 구한 해를 활용한다. (메모이제이션)

이전의 해를 활용해야 효율적인 문제의 조건

  • 최적 부분 구조(Optimal Substructure)
    • 문제의 최적 해결책이 하위 문제의 최적 해결책으로 부터 구성되는 경우
  • 중복 부분 문제(Overlapping Subproblems)
    • 동일한 하위 문제가 여러번 계산 됨

예시 1 : 팩토리얼

  • 동적 계획법으로 풀어도 효율이 없다.
  • 크기 N의 문제를 크기 (N - 1) 문제 해로 해결
  • Fact(N - 1)은 Fact(N)의 부분 해(최적 부분 구조)
  • 동일한 하위 문제가 반복되지 않음 (중복 부분 문제는 아니다.)
  • 최적 부분 구조라서 동적 계획법으로 풀 수는 있다.
    • 중복 부분 문제가 아니라서 효율적이지 않다.

예시 2 : 피보나치 수

  • 동적 계획법으로 풀면 효율적이다.
  • 크기 N의 문제를 크기 (N - 1) 문제와 (N - 2) 문제의 해로 해결
  • Fibo(N - 1)은 Fibo(N)의 부분 해(최적 부분 구조)
  • Fibo(5)를 구하는 과정에서 Fibo(3)이 2번 나옴
    • 즉, 이전해가 반복된다. (중복 부분 문제)
    • Fibo(N) = Fibo(N - 1) + Fibo(N - 2)
    • Fibo(N - 1) = Fibo(N - 2) + Fibo(N - 3)
    • Fibo(N - 2) = Fibo(N - 3) + Fibo(N - 4)
  • 최적 부분 구조이자, 중복 부분 문제다.
    • 동적 계획법으로 효율적으로 문제를 풀 수 있다.

동적 계획법 접근법

  • 예제 입력으로 출력 만드는 과정을 직접 손으로 작성
  • 과정을 일반화 한다.
    • 최종해를 구하는 과정을, 이전해를 구하는 과정을 통해 나타낼 수 있는지 확인
    • 최적 부분 구조로 나타낼 수 있는지 확인한다.
  • 두 번째 과정에서 이전해를 구하는 과정이 중복되는지 확인한다.

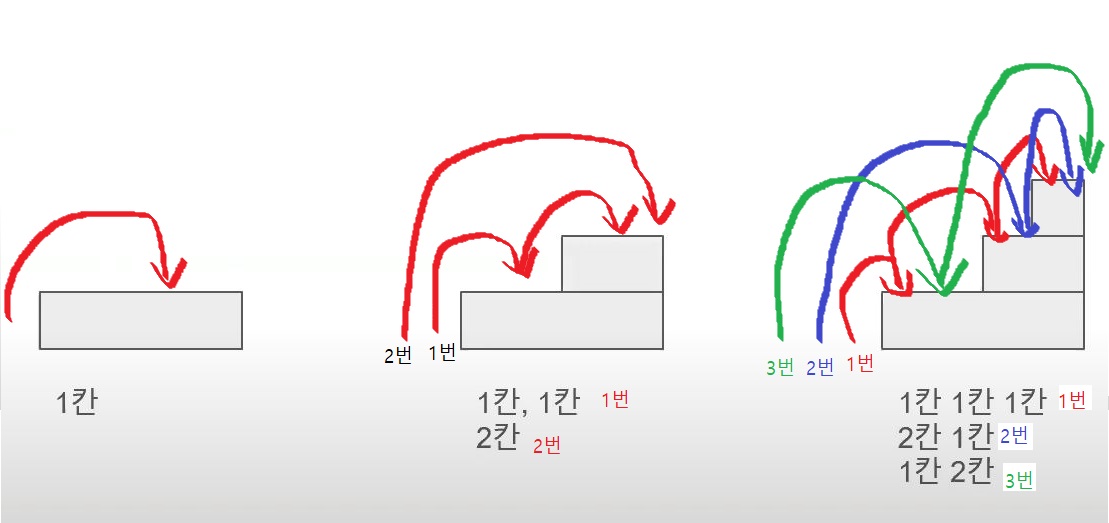
예시 1 : 계단 오르기

  • algorithm-study
  • N개의 계단이 존재하고, 한 번에 1개 혹은 2개의 계단을 오를 수 있다. 계단을 오르는 방법의 총 수는?
  • 3개의 계단을 오를 때, 2개를 오를 때와 1개를 오를 때 사용했던 해를 사용한다.
    • F(3) = F(2) + F(1)
  • 직접 구해야 하는 해를 기저 조건이라고 한다.
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

      import java.util.Scanner;
                                                                          //
  public class Main {
      public static void main(String[] args) {
          Scanner sc = new Scanner(System.in);
                                                                          //
          System.out.print("계단의 수를 입력하세요: ");
          int n = sc.nextInt();
                                                                          //
          int result = countWays(n);
          System.out.println("계단을 오르는 방법의 총 수: " + result);
      }
                                                                          //
      // 계단을 오르는 방법의 총 수를 계산하는 함수
      public static int countWays(int n) {
          // 동적 계획법을 위한 배열 선언
          int[] dp = new int[n + 1];
                                                                          //
          // 초기값 설정
          dp[1] = 1; // 계단 1개를 오르는 방법은 1가지
          if (n >= 2) {
              dp[2] = 2; // 계단 2개를 오르는 방법은 2가지 (1+1 또는 2)
          }
                                                                          //
          // 동적 계획법을 이용한 계산
          // 점화식: dp[i] = dp[i - 1] + dp[i - 2]
          for (int i = 3; i <= n; i++) {
              dp[i] = dp[i - 1] + dp[i - 2];
          }
                                                                          //
          return dp[n];
      }
  }

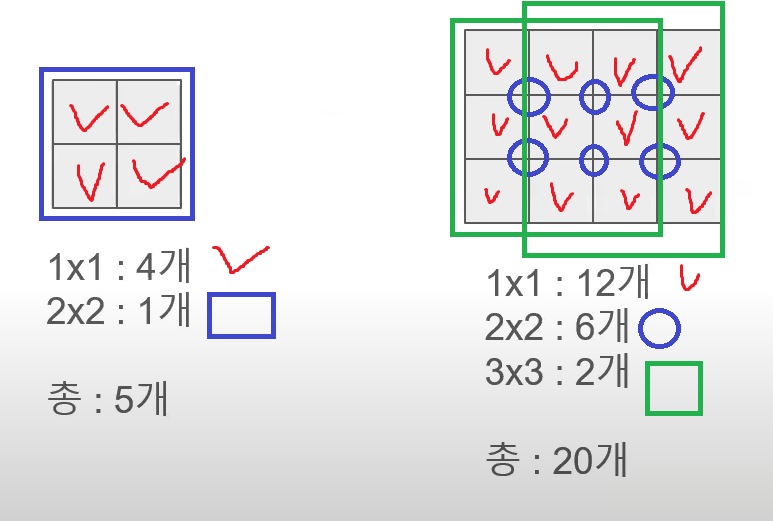
예시 2 : 만들 수 있는 정사각형 갯수

  • algorithm-study
  • 사각형이 주어질 때, 만들 수 있는 정사각형의 갯수 확인
  • 2x2 사각형을 만들 때는 1x1 4개를 썼다.
    • 3x3 사각형을 만들 때는 2x2 4개를 썼다.
    • 즉, 1x1로도 2x2, 3x3을 만들 수 있다.
  • 현재 칸 기준 사각형의 왼쪽 / 위 / 왼쪽 위 대각선에서 크기가 N인 정사각형을 만들 수 있다면
    • N + 1 크기의 정사각형을 만들 수 있다.
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

      import java.util.Arrays;
                                                                                      //
  public class Main {
      // 행과 열의 상수 선언
      static final int ROW = 3;
      static final int COL = 4;
                                                                                      //
      public static void main(String[] args) {
          int result = countSquares();
          System.out.println("만들 수 있는 정사각형의 총 개수: " + result);
      }
                                                                                      //
      // ROW x COL 크기의 사각형에서 만들 수 있는 모든 정사각형의 개수를 계산하는 함수
      public static int countSquares() {
          int[][] dp = new int[ROW][COL];
                                                                                      //
          // 모든 값을 1로 초기화
          for (int[] row : dp) {
              Arrays.fill(row, 1);
          }
                                                                                      //
          // 동적 계획법을 이용한 계산
          for (int i = 1; i < ROW; i++) {
              for (int j = 1; j < COL; j++) {
                  // dp[i][j]는 현재 셀에서 만들 수 있는 가장 큰 정사각형의 크기를 나타냄
                  dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1;
              }
          }
                                                                                      //
          int totalSquares = 0;
          // 모든 dp 값 합산
          for (int i = 0; i < ROW; i++) {
              for (int j = 0; j < COL; j++) {
                  totalSquares += dp[i][j];
              }
          }
                                                                                      //
          return totalSquares;
      }
  }

예시 3 : 최장 증가 부분 수열(LIS)

  • 부분 수열
    • 주어진 수열 중 일부를 뽑아 새로만든 수열(이 때 순서는 유지)
  • 최장 증가 부분 수열
    • 주어진 수열 중 일부를 뽑아 새로만든 부분 수열 중, 오름차순을 유지(엄격한 증가)하면서 가장 긴 수열
    • 한 번에 전체 해를 구하는 것은 어렵다.
  • 각 배열의 원소로 끝나는 LIS를 구해보자.
    • 배열[] = 1, 4, 2, 3, 1, 5, 7, 3
    • 1
    • 1, 4
    • 1, 4, 2
    • 1, 4, 2, 3
    • 1, 4, 2, 3, 1
    • 1, 4, 2, 3, 1, 5
    • 1, 4, 2, 3, 1, 5, 7
    • 1, 4, 2, 3, 1, 5, 7, 3
  • K번째 위치의 LIS를 LIS(K)라고 한다면, X번째 원소는 K번째 원소보다 작다. (1 <= X < K)
    • 맨 뒤에 K번째 원소가 와야 하기 때문이다.
  • 앞에서 찾은 특정 원소로 끝나는 LIS 길이 중 가장 큰 것에 1을 더하면 된다.
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

      import java.util.*;
                                                                                      //
  public class Main {
                                                                                      //
      // 동적 계획법을 사용하여 최장 증가 부분 수열(LIS)을 계산하는 함수
      public static int lis(int[] arr) {
          int n = arr.length;
          int[] dp = new int[n];
          Arrays.fill(dp, 1); // 각 원소를 초기값 1로 초기화
                                                                                      //
          // LIS 계산
          for (int i = 1; i < n; i++) { // arr[i]를 마지막 원소로 하는 LIS 계산
              for (int j = 0; j < i; j++) { // arr[j] (0 <= j < i)를 마지막 원소로 하는 LIS 고려
                  if (arr[i] > arr[j] && dp[i] < dp[j] + 1) { // arr[i]가 arr[j]보다 크고 dp[i]가 dp[j] + 1보다 작으면
                      dp[i] = dp[j] + 1; // dp[i] 갱신
                  }
              }
          }
                                                                                      //
          // dp 배열 중 최댓값이 LIS 길이
          int lisLength = 0;
          for (int len : dp) {
              lisLength = Math.max(lisLength, len);
          }
                                                                                      //
          return lisLength;
      }
                                                                                      //
      public static void main(String[] args) {
          int[] arr = {10, 22, 9, 33, 21, 50, 41, 60, 80}; // 예시 배열
          System.out.println("LIS 길이: " + lis(arr));
      }
  }

가장 큰 정사각형 찾기 문제 풀이

땅따먹기 문제 풀이

정수 삼각형 문제 풀이

Algorithm, Study
java algorithm study