Post

[코딩테스트 합격자 되기 스터디] 8주차 - 정렬 (8.25 ~ 8.31)

Posted Updated
By Je Hun Lim 10 min read

코딩테스트 합격자 되기 스터디 8주차

강의 보기 -> 해당되는 부분 책 다시 읽기 -> 블로그 정리
강의는 C++로 되어 있지만 개념적인 내용이라 언어 상관 없이 보고 코드는 각 언어에 맞게 바꾸면 된다.

참고 강의 및 책

인프런 : 코딩테스트 합격자 되기 파이썬, C+_+ 저자님 인프런 강의 링크
Youtube : 코딩테스트 합격자 되기 파이썬, C+_+ 저자님 Youtube 링크
종이책 : 코딩테스트 합격자 되기 파이썬 편
종이책 : 코딩테스트 합격자 되기 C++ 편
종이책 : 코딩테스트 합격자 되기 자바스크립트 편
종이책 : 코딩테스트 합격자 되기 자바 편

정렬

  • 데이터를 특정 기준에 따라 순서대로 배치
    • 오름차순(작은 값부터 큰 값으로), 1 3 4
    • 내림차순(큰 값부터 작은 값으로), 4 3 1

코딩테스트에서 정렬은 언제 필요한가?

  • 정렬된 상태에서 동작하는 알고리즘을 사용해야 하는 경우
    • 이진 탐색은 정렬이 되어 있어야 할 수 있다.
    • 병합정렬의 병합
  • 알고리즘을 써야 하는데 알고리즘의 전제 조건이 정렬이 된 상태인 경우가 많다.

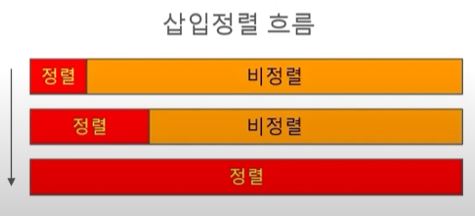
정렬 알고리즘 - 삽입정렬

  • 왼쪽은 정렬된 영역, 오른쪽은 비 정렬된 영역으로 나누어진다.
  • 정렬된 영역이 점점 확장되어 비 정렬된 영역이 없어지는 정렬 방법
  • 비 정렬된 영역의 맨 앞의 원소를 정렬된 영역의 적절한 곳에 추가
  • 맨 앞의 원소를 정렬 영역의 정렬 상태를 유지할 수 있는 위치에 삽입한다.
  • algorithm-study
  • 1 5 2 3 으로 정렬이 되어있다.
    • 1과 5를 비교한다. 5가 1보다 크기 때문에 제자리에 둔다. 1 5 2 3
    • 5와 2를 비교한다. 5가 2보다 크기 때문에 5를 오른쪽으로 이동시킨다. 1 ? 5 3
    • 1과 2를 비교한다. 2가 1보다 크기 때문에 ? 자리에 2를 삽입한다. 1 2 5 3
    • 5와 3을 비교한다. 5가 3보다 크기 때문에 5를 오른쪽으로 이동시킨다. 1 2 ? 5
    • 2와 3을 비교한다. 3이 2보다 크기 때문에 ? 자리에 3을 삽입한다. 1 2 3 5
    • 1 2 3 5로 정렬이 끝났다.
  • 삽입정렬의 최악의 케이스
    • 5 4 3 2 1, 역정렬된 경우
    • 5와 4를 비교한다. 1칸 움직인다. 1번 비교, 4 5 3 2 1
    • 3과 5, 4를 비교한다. 2칸 움직인다. 2번 비교, 3 4 5 2 1
    • 2와 5, 4, 3을 비교한다. 3칸 움직인다. 3번 비교, 2 3 4 5 1
    • 1과 5, 4, 3, 2를 비교한다. 4칸 움직인다. 4번 비교, 1 2 3 4 5
    • 시간 복잡도 O(N^2)
  • 삽입정렬의 최선의 케이스
    • 1 2 3 4 5, 처음부터 정렬된 경우
    • 1과 2를 비교한다. 움직이지 않는다. 1번 비교, 1 2 3 4 5
    • 2와 3을 비교한다. 움직이지 않는다. 1번 비교, 1 2 3 4 5
    • 3와 4을 비교한다. 움직이지 않는다. 1번 비교, 1 2 3 4 5
    • 4와 5을 비교한다. 움직이지 않는다. 1번 비교, 1 2 3 4 5
    • 시간 복잡도 O(N)
  • 정렬 대상이 어떻게 배치되어 있냐에 따라 성능이 달라진다.

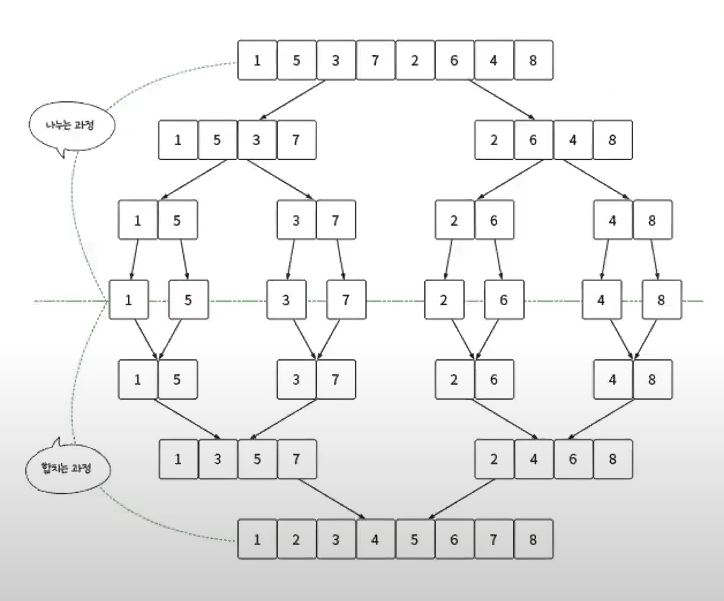
정렬 알고리즘 - 병합정렬

  • 리스트를 반으로 나누어 각각 정렬한 뒤, 합치는 방식
  • 각 부분 리스트를 재귀적으로 정렬
  • 최종적으로 정렬된 두 리스트를 합쳐서 전체 리스트 정렬
  • algorithm-study
    • 원소가 한 개가 될 때 까지 반으로 계속 나눈다.
    • 배열을 물리적으로 나누는 것은 아니다.
    • 인덱스를 활용해서 나누어진 것 처럼 동작
    • 정렬을 하면서 합친다.
  • divide & conquer 알고리즘이라고도 한다.
    • 나누고 병합
  • 정렬이 되어 있어야 한다.

정렬 알고리즘 - 힙정렬

  • 힙
    • 최대힙 : 부모노드가 자식노드보다 항상 크다.
    • 최소힙 : 부모노드가 자식노드보다 항상 작다.
  • 원본 데이터 -> 힙 구축 -> 힙 정렬
  • 힙 구축하기 (노드 번호 N/2 부터 1까지 차례대로 시행)
    • 현재 노드와 자식 노드 비교(자식 노드가 없다면 연산 종료)
    • 현재 노드가 가장 크지(작지) 않다면, 가장 큰(작은) 자식 노드의 값과 바꾼다.
    • 맞바꾼 자식 노드 위치를 현재노드로 해서 1부터 반복
    • N/2 부터 하는 이유는 N/2보다 큰 노드는 자식이 없다.
  • 힙 정렬
    • 정렬되지 않은 데이터로 최대(소)힙 구축
    • 현재 최대(소)힙의 루트노드와 마지막 노드를 바꾼다.
    • 최대(소)힙 사이즈가 1이면 종료, 최대(소)힙 사이즈를 1 줄인다.
    • 힙 구축하기, max_heapify(1) 수행, 다시 2로 간다.
    • 힙 사이즈가 1일 때 까지 반복한다.

우선순위 큐

  • 기존 큐는 FIFO로 동작
  • 우선순위 큐는 입력 순서와 상관없이 우선순위가 높은 원소가 먼저 출력된다.
  • 구현 시 고려할 점
    • 원소가 계속 들어오는 상황에서 정렬 상태를 유지 해야한다.
    • 기존 대부분 정렬 방법은 O(NlogN)
    • 힙정렬을 사용할 경우 삽입/삭제시 O(logN) 보장, 우선순위 큐는 힙을 사용
  • 코딩테스트에서 우선순위 큐는 최단경로 알고리즘(다익스트라, 밸만포드) 구현 시 많이 사용된다.
  • 기본적으로 최대힙으로 동작한다. (자바는 최소힙)
    • 10, 30, 20, 5를 순서대로 푸시한다.
    • 30, 20, 10, 5 순서대로 팝된다. (최대 힙)
    • 자바는 5, 10, 20, 30 순서대로 팝된다.
  • 우선순위를 따로 제공할 수도 있다. (사용자 정의타입은 필수)
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

      import java.util.PriorityQueue;
                                                                                      //
  public class Main {
      public static void main(String[] args) {
          // PriorityQueue 선언 (기본적으로 최소 힙)
          PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a); // 최대 힙을 위해 Comparator 사용
                                                                                                          //
          // offer: O(log n)
          pq.offer(3);
          pq.offer(1);
          pq.offer(4);
                                                                                                          //
          // peek: O(1)
          System.out.println(pq.peek());  // 출력: 4 (가장 높은 우선순위)
                                                                                                          //
          // poll: O(log n)
          pq.poll();
                                                                                                          //
          // size: O(1)
          System.out.println(pq.size());  // 출력: 2
                                                                                                          //
          // 순회 (힙의 순서대로, 정렬된 순서가 아님): O(n)
          while(!pq.isEmpty()) {
              System.out.print(pq.peek() + " ");  // 출력: 3 1
              pq.poll();
          }
          System.out.println();
                                                                                                          //
          // clear: PriorityQueue의 clear 메서드를 사용할 수 있습니다.
          pq.clear();
      }
  }

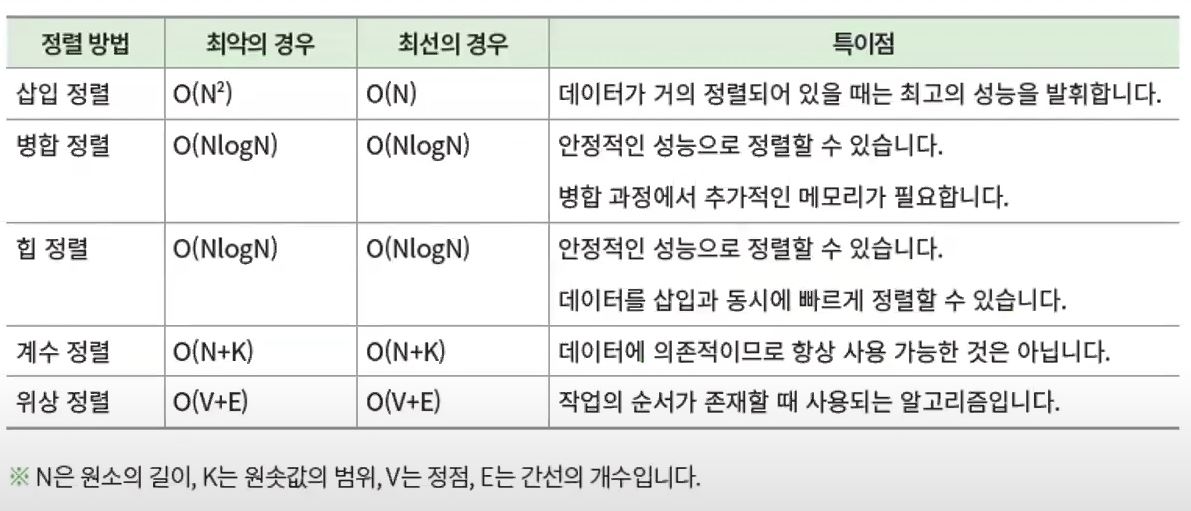
각 정렬 알고리즘 비교

  • algorithm-study

문자열 내 마음대로 정렬하기 문제 풀이

지형 이동 문제 풀이

Algorithm, Study
java algorithm study