Post

[코딩테스트 합격자 되기 스터디] 6주차 - 그래프 (8.11 ~ 8.17)

Posted Updated
By Je Hun Lim 40 min read

코딩테스트 합격자 되기 스터디 6주차

강의 보기 -> 해당되는 부분 책 다시 읽기 -> 블로그 정리
강의는 C++로 되어 있지만 개념적인 내용이라 언어 상관 없이 보고 코드는 각 언어에 맞게 바꾸면 된다.

참고 강의 및 책

인프런 : 코딩테스트 합격자 되기 파이썬, C+_+ 저자님 인프런 강의 링크
Youtube : 코딩테스트 합격자 되기 파이썬, C+_+ 저자님 Youtube 링크
종이책 : 코딩테스트 합격자 되기 파이썬 편
종이책 : 코딩테스트 합격자 되기 C++ 편
종이책 : 코딩테스트 합격자 되기 자바스크립트 편
종이책 : 코딩테스트 합격자 되기 자바 편

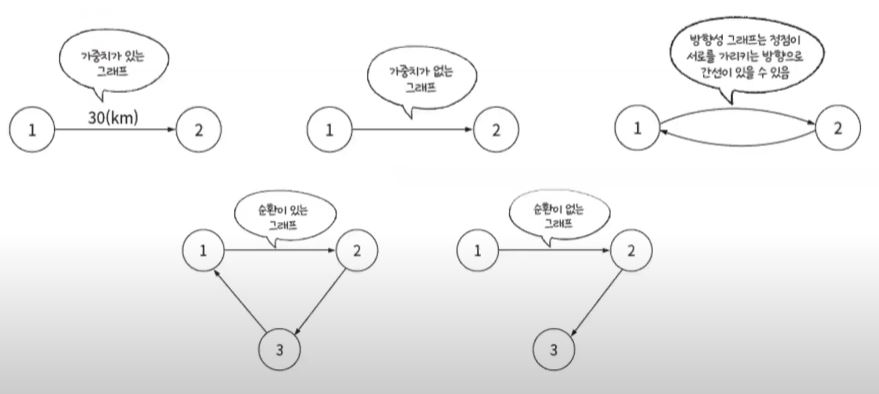
그래프

  • 노드와 간선을 이용한 비선형 자료구조
    • 목적에 따라 간선의 가중치나 방향이 있을 수 있다
  • 그래프의 종류
    • 가중치가 있는 그래프
    • 가중치가 없는 그래프
    • 방향성 그래프
    • 순환이 있는 그래프
    • 순환이 없는 그래프
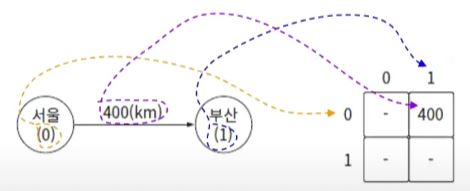
  • algorithm-study

그래프의 구현 - 인접 행렬

  • 2차원 배열로 표현한다.
  • 행과 열의 인덱스로 노드의 값을 나타내고, 배열의 값은 간선의 가중치가 된다.
  • algorithm-study
    • 보라색은 가중치다.
    • 서울(0), 부산(1)은 노드다.
    • 서울에서 부산 방향으로 가는 간선의 가중치는 400이라는 뜻이다.
    • 서울(0)에서 부산(1) 방향이니 배열[0][1]에 가중치 400을 대입한다.
  • 노드 대비 간선이 적을 경우 메모리 공간 효율이 좋지 않다.
    • 노드 100개가 있어도 위 이미지처럼 간선이 한 개만 있는 경우에도 배열[100][100]이 필요하다.
    • 노드가 1 -> 2 -> 100 으로 간선이 2개가 있어도 배열[100][100]이 필요하다.
    • 즉, 100x100 행렬이 필요하다. (메모리 낭비)
  • 특정 노드 사이 간선 존재 여부를 한 번에 알 수 있다.
    • 0에서 4까지 간선이 있는가?
    • 배열[0][4] 값을 확인하면 한 번에 알 수 있다.
  • 가중치가 없는 그래프라면 간선이 있으면 1, 없으면 0으로 표기한다.
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

      import java.util.Arrays;
  public class AdjacencyMatrix {
      // 인접 행렬의 노드 개수 (고정)
      static final int numNodes = 2;
      // 인접 행렬 배열
      static int[][] adjMatrix = new int[numNodes][numNodes];
      // 인접 행렬을 초기화하는 함수 모든 값을 0으로 설정
      public static void initializeMatrix() {
          for (int i = 0; i < numNodes; i++) {
              Arrays.fill(adjMatrix[i], 0);
          }
      }
      // 간선을 추가하는 함수, u에서 v로 가는 간선의 가중치를 설정
      public static void addEdge(int u, int v, int weight) {
          adjMatrix[u][v] = weight;
      }
      // 인접 행렬을 출력하는 함수, 값이 0인 경우 '-'로 출력
      public static void printMatrix() {
          for (int i = 0; i < numNodes; i++) {
              for (int j = 0; j < numNodes; j++) {
                  if (adjMatrix[i][j] == 0)
                      System.out.print("- ");
                  else
                      System.out.print(adjMatrix[i][j] + " ");
              }
              System.out.println();
          }
      }
      public static void main(String[] args) {
          // 인접 행렬 초기화
          initializeMatrix();
          // 엣지 추가: 서울(0)에서 부산(1)으로 가는 엣지, 가중치 400
          addEdge(0, 1, 400);
          // 인접 행렬 출력
          printMatrix();
      }
  }

그래프의 구현 - 인접 리스트

  • 특정 시작 노드를 기준으로 연결된 노드들을 리스트로 연결하는 방식
  • 실제 그래프의 노드 갯수만큼만 추가하므로 메모리 낭비가 없다.
  • 특정 노드에 모든 노드가 연결된 경우, 탐색 시 O(N)이 될 수 있다.
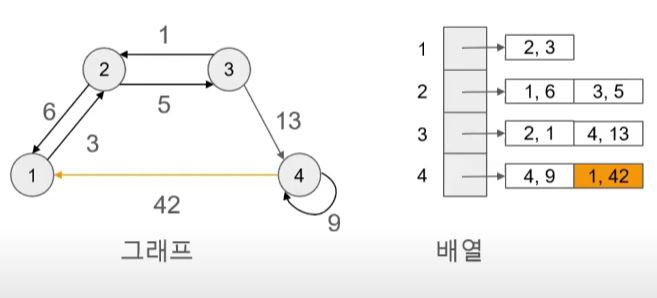
  • 인접 리스트 표현 방식
    • 노드 개수 만큼 배열을 준비한다.
    • 각 배열의 인덱스는 시작 노드를 나타낸다.
    • 해당 인덱스에 연결된 노드 추가
  • algorithm-study
    • 시작 노드1에서 2까지 가는 가중치가 3인 간선을 인접 리스트에 추가한다.
    • 2에서 1까지 가는 가중치가 6인 간선을 인접 리스트에 추가한다.
    • 2에서 3까지 가는 가중치가 5인 간선을 인접 리스트에 추가한다.
    • 3에서 2까지 가는 가중치가 1인 간선을 인접 리스트에 추가한다.
    • 3에서 4까지 가는 가중치가 13인 간선을 인접 리스트에 추가한다.
    • 4에서 4까지 가는 가중치가 9인 간선을 인접 리스트에 추가한다.
    • 4에서 1까지 가는 가중치가 42인 간선을 인접 리스트에 추가한다.
    • 왼 쪽에 있는 그래프를 인접 리스트로 표현하면 오른쪽과 같이 된다.
    • 그래프의 간선이 7개, 인접 리스트에 있는 간선도 7개다.
    • 그래프 구성 요소만 인접 리스트에 추가하기 때문에 메모리 낭비가 없다.
    • 리스트를 사용하기 때문에 추가와 삭제가 상대적으로 용이하다.
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

      import java.util.ArrayList;
  import java.util.List;
  public static void main(String[] args) {
      // 정점의 수
      int V = 4;
      // 인접 리스트 생성
      List<List<int[]>> adjList = new ArrayList<>();
      // 인접 리스트 초기화
      for (int i = 0; i <= V; i++) {
          adjList.add(new ArrayList<>());
      }
      // 간선 정보 (시작 정점, 끝 정점, 가중치)
      int[][] edges = {
          {1, 2, 3},
          {1, 3, 5},
          {2, 1, 6},
          {2, 3, 5},
          {3, 2, 1},
          {3, 4, 13},
          {4, 4, 9},
          {4, 1, 42}
      };
      // 그래프에 간선 추가
      for (int[] edge : edges) {
          int u = edge[0]; // 시작 정점
          int v = edge[1]; // 끝 정점
          int weight = edge[2]; // 가중치
          adjList.get(u).add(new int[]{v, weight});
      }
      // 인접 리스트 출력
      for (int i = 1; i <= V; ++i) {
          System.out.print("Vertex " + i + ":");
          for (int[] edge : adjList.get(i)) {
              System.out.print(" (" + edge[0] + ", " + edge[1] + ")");
          }
          System.out.println();
      }
  }

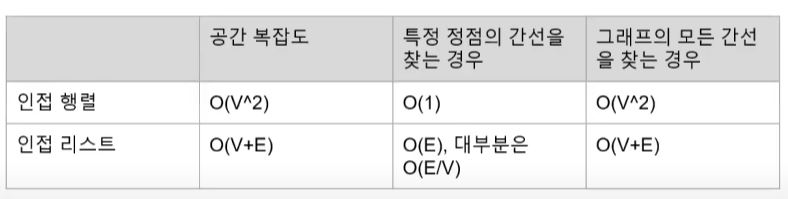
인접 행렬 VS 인접 리스트

  • algorithm-study
  • 노드의 개수가 많을 때는 인접 리스트를 써야한다.
    • 인접 행렬 사용 시 메모리 초과 가능성이 있다.
  • 인접 행렬
    • 특정 정점의 간선을 빠르게 찾을 수 있다.
  • 인접 리스트
    • 공간 복잡도가 낮다.
    • 그래프의 모든 간선을 찾는 경우 인접 행렬보다 빠르다.
  • 무엇을 써야할 지 모른다면 먼저 인접 리스트로 구현 하는 게 유리하다.

그래프의 탐색

  • 그래프를 정해진 순서로 순회하는 방법
  • 깊이 우선 탐색(DFS)
    • 더 이상 탐색할 노드가 없을 때 까지 방문한다.
    • 더 이상 탐색할 노드가 없다면 최근에 방문했던 노드로 돌아가고, 가지 않은 노드 방문
  • 너비 우선 탐색(BFS)
    • 현재 위치에서 가장 가까운 노드부터 방문하고 다음 노드로 넘어간다.
    • 모든 노드를 방문할 때 까지 위 과정 반복

그래프의 탐색 - 깊이 우선 탐색(DFS)

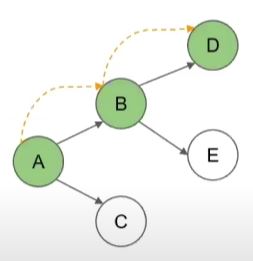
  • algorithm-study
    • A -> B -> D 순차적으로 방문
    • D 다음 탐색할 노드가 없다.
    • D를 방문하기 전에 가장 최근에 방문한 B로 돌아간다. A -> B -> D -> B
    • B에서 아직 방문하지 않은 노드가 있으니 깊이 들어간다.
    • 노드 E를 방문한다. A -> B -> D -> B -> E
    • E 다음 탐색할 노드가 없다.
    • E를 방문하기 전에 가장 최근에 방문한 B로 돌아간다. A -> B -> D -> B -> E -> B
    • B 다음 탐색할 노드가 없다.
    • B를 방문하기 전에 가장 최근에 방문한 A로 돌아간다. A -> B -> D -> B -> E -> B -> A
    • A에서 아직 방문하지 않은 노드가 있으니 깊이 들어간다.
    • 노드 C를 방문한다. A -> B -> D -> B -> E -> B -> A -> C
    • C 다음 탐색할 노드가 없다.
    • 모든 노드를 방문했으니 탐색을 종료한다.
    • 최종 방문 순서 A -> B -> D -> E -> C
  • 다른 탐색 대비 깊이 우선 탐색이 가지는 가장 중요한 특징이 백트래킹이다.
    • 위 사진 내용에서 최근 방문한 곳으로 돌아가는 것을 백트래킹이라 한다.
  • 깊이 우선 탐색 구현하기
    • 계속해서 깊이 탐색할 수 있어야 한다.
    • 더 이상 깊은 곳이 없는 경우, 가장 최근에 방문했던 노드로 돌아갈 수 있어야 한다.
    • 이미 방문한 노드는 중복해서 방문하지 않아야 한다.
  • 가장 최근에 방문했던 노드로 가는 효율적인 방법
    • LIFO로 동작하는 스택을 활용한다.
    • 방문할 노드 푸시, 방문한 노드는 팝, 스택의 top은 가장 최근에 방문한 노드
    • stack이 함수 호출 흐름과 동일하기 때문에 재귀 함수로 구현하는 경우가 많다.
    • visited 배열을 활용해서 방문 여부를 확인 후에 노드를 탐색한 후 방문한다.
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

      import java.util.ArrayList;
  import java.util.List;
  public class DFSExample {
      // 인접 리스트 및 방문 리스트
      private static List<Integer>[] adj;
      private static boolean[] visited;
      public static void main(String[] args) {
          int V = 5;  // 정점의 개수
          // 인접 리스트 초기화
          adj = new ArrayList[V];
          for (int i = 0; i < V; i++) {
              adj[i] = new ArrayList<>();
          }
          // 그래프의 간선 정보 (각 배열의 첫 번째 값이 시작 정점, 두 번째 값이 도착 정점)
          int[][] edges = {
              {0, 1}, // A -> B
              {0, 2}, // A -> C
              {1, 3}, // B -> D
              {1, 4}  // B -> E
          };
          // 인접 리스트에 간선 추가
          for (int[] edge : edges) {
              addEdge(edge[0], edge[1]);
          }
          // 방문 배열 초기화
          visited = new boolean[V];
          System.out.println("깊이 우선 탐색 (정점 0에서 시작):");
          // DFS 수행
          dfs(0);
          /*
              재귀 호출 과정 설명 (예: 정점 0에서 시작):
              dfs(0) 호출 -> 0 출력
                  dfs(1) 호출 -> 1 출력
                      dfs(3) 호출 -> 3 출력
                      dfs(4) 호출 -> 4 출력
                  dfs(2) 호출 -> 2 출력
              - dfs_traversal 종료
          */
      }
      private static void addEdge(int v, int w) {
          adj[v].add(w); // 정점 v의 인접 리스트에 정점 w를 추가
      }
      private static void dfs(int v) {
          // 현재 정점을 방문했다고 표시하고 출력
          visited[v] = true;
          System.out.print(v + " ");
          // 현재 정점에 인접한 모든 정점을 순회
          for (int w : adj[v]) {
              if (!visited[w]) {
                  dfs(w);
              }
          }
      }
  }

그래프의 탐색 - 너비 우선 탐색(BFS)

  • algorithm-study
    • A 방문
    • A에서 가장 가까운 노드 B, C를 방문 (간선 1개를 거친다) A -> B -> C
    • 2개의 간선을 거치는 D, E를 방문한다. A -> B -> C -> D -> E
    • 모든 노드를 방문했으니 탐색을 끝낸다.
  • 너비 우선 탐색 구현하기
    • 루트 노드부터 시작해서, 가장 가까운 노드들부터 방문할 수 있어야 한다.
    • 루트 -> 1개 간선으로 갈 수 있는 노드 -> 2개 간선으로 갈 수 있는 노드…(모든 노드 방문할 때 까지 반복)
  • 가장 가까운 노드부터 방문하는 효율적인 방법
    • FIFO로 동작하는 큐를 활용한다.
    • 시작 노드 푸시
    • 팝 후에 방문 처리 이후, 현재 노드에서 연결된 노드 중 방문하지 않은 노드 모두 푸시
    • 모든 노드를 방문할 때 까지 반복한다.
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

      import java.util.ArrayList;
  import java.util.LinkedList;
  import java.util.List;
  import java.util.Queue;
  public class BFSExample {
      private static List<Integer>[] adj;  // 인접 리스트를 배열로 정의
      private static boolean[] visited;    // 방문 여부를 기록하는 배열
      // 그래프에 간선을 추가하는 메서드
      private static void addEdge(int u, int v) {
          adj[u].add(v); // 정점 u의 인접 리스트에 정점 v를 추가
      }
      // 너비 우선 탐색(BFS)을 수행하는 메서드
      private static void bfs(int start) {
          Queue<Integer> q = new LinkedList<>();
          visited[start] = true;
          q.add(start);
          while (!q.isEmpty()) {
              int v = q.poll();
              System.out.print(v + " ");
              for (int w : adj[v]) {
                  if (!visited[w]) {
                      visited[w] = true;
                      q.add(w);
                  }
              }
          }
      }
      public static void main(String[] args) {
          int V = 5; // 정점의 개수
          adj = new ArrayList[V];
          for (int i = 0; i < V; i++) {
              adj[i] = new ArrayList<>(); // 각 정점의 인접 리스트를 초기화
          }
          // 그래프의 간선 정보 (각 배열의 첫 번째 값이 시작 정점, 두 번째 값이 도착 정점)
          int[][] edges = {
              {0, 1}, // A -> B
              {0, 2}, // A -> C
              {1, 3}, // B -> D
              {1, 4}  // B -> E
          };
          // 인접 리스트에 간선 추가
          for (int[] edge : edges) {
              addEdge(edge[0], edge[1]);
          }
          visited = new boolean[V]; // 방문 배열 초기화
          System.out.println("너비 우선 탐색 (정점 0에서 시작):");
          bfs(0);
          /*
          BFS 호출 과정 설명 (예: 정점 0에서 시작):
          1. bfs(0) 호출 -> 0 출력, 인접 정점 1과 2를 큐에 추가
          2. 큐에서 1을 꺼내어 출력 -> 인접 정점 3과 4를 큐에 추가
          3. 큐에서 2를 꺼내어 출력 -> 인접 정점 없음
          4. 큐에서 3을 꺼내어 출력 -> 인접 정점 없음
          5. 큐에서 4를 꺼내어 출력 -> 인접 정점 없음
          6. 큐가 비어 있으므로 탐색 종료
          */
      }
  }

깊이 우선 탐색(DFS) VS 너비 우선 탐색(BFS)

  • 백트래킹은 깊이 우선 탐색(DFS)에만 존재
    • 스도쿠 문제, 1 ~ 5를 사용해서 합이 10이 되는 모든 경우 등
  • 너비 우선 탐색으로 찾은 해만 최적의 해를 보장한다.
    • 시작점에서 끝지점까지 가는데 최소한의 움직임
  • 너비 우선 탐색은 모든 다음 노드를 큐에 푸쉬하므로 깊이 우선 탐색보다 메모리 사용량이 높다.
  • 둘 다 되는 경우가 존재, 애매하면 깊이 우선 탐색 먼저 시도한다.

최단 경로 알고리즘

  • 두 노드를 잇는 가중치의 합을 최소로 하는 경로를 찾는 알고리즘

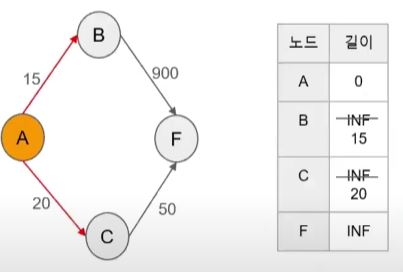
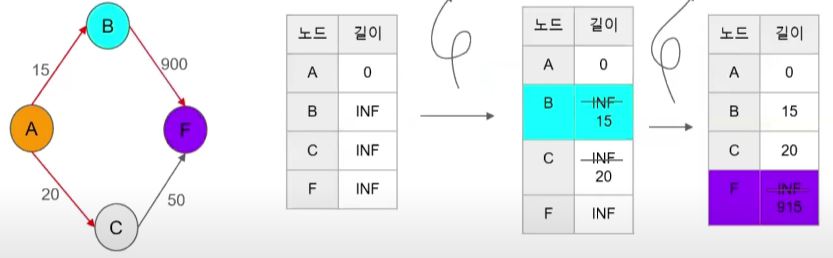
최단 경로를 구하기 위한 아이디어1

  • algorithm-study
    • 시작 노드는 A, 최소 비용은 0
    • A에서 바로갈 수 있는 노드는 B와 C
    • A -> B는 최소 비용 15, A -> C는 최소 비용 20으로 A -> B 최소 비용이 가장 적다.
    • 간선의 가중치가 모두 양수라면, A -> B 경로는 갱신될 경우가 없다.

최단 경로를 구하기 위한 아이디어2

  • algorithm-study
    • A -> B가 최소 비용 중의 최소 비용이다.
    • 현재 까지 구한 최소 비용 중의 최소 비용을 후보 노드라고 한다.
    • 후보 노드 까지는 고정이다. 왜냐면 다른 노드로 가도 후보 노드 보다 비용이 크기 때문이다.
    • B -> F는 후보 노드 까지의 비용 + 다음 노드로 가는 가중치 이다.
    • F 노드에 설정되어 있는 최소 비용과, F 노드까지 가는 최소 비용을 비교하여 더 적은 비용으로 갱신한다.
    • 이 과정을 모든 정점에 대해 한 번씩 수행하면, 시작 노드에서 각 정점의 노드까지 최소 비용을 구할 수 있다.

다익스트라 알고리즘으로 실제 최단 경로 구하기

  • 다익스트라 알고리즘
    • 가중치가 있는 그래프에서 특정 시작 노드로부터 다른 모든 노드까지의 최단 경로를 찾는 알고리즘
    • 그래프의 모든 간선의 가중치가 양수일 때 유효
    • 음수 가중치를 가진 간선이 있는 그래프에서는 동작하지 않는다.
    • 음수 가중치가 있는 경우 벨만-포드 알고리즘을 사용해야 한다.
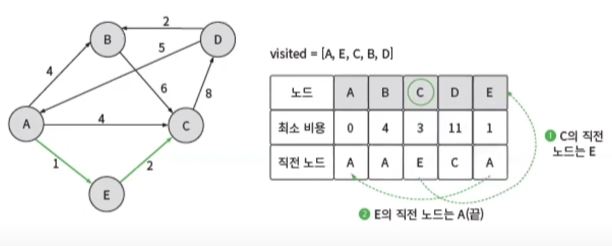
  • algorithm-study
    • 시작 노드 A, A를 후보 노드로 설정하고 visited에 추가한다. visited[A]
    • A에서 갈 수 있는 노드 A -> B(4), A -> C(4), A -> E(1) 최소 비용, 직전 노드 갱신
    • 후보 노드 A를 제외 하고, 최소 비용이 제일 적은 E가 다음 후보 노드가 된다.
    • E를 후보 노드로 설정하고 visited에 E를 추가한다. visited[A, E]
    • E에서 갈 수 있는 노드들 중, 최단 경로를 갱신할 수 있는 노드를 확인한다.
    • E -> C(2) 이고, (E까지 가는 최소 비용 1) + (E -> C까지 가는 최소 비용 2)로 C 노드에 저장된 최소 비용과 비교한다.
    • C의 현재 최소 비용은 4이다. 3 < 4 이기 때문에 C의 최소 비용을 3으로 갱신한다.
    • C가 갱신될 때 직전 노드는 E이다. 직전 노드도 E로 갱신한다.
    • 후보 노드 A, E를 제외하고, 최소 비용이 제일 적은 C가 다음 후보 노드가 된다.
    • C를 후보 노드로 설정하고 visited에 C를 추가한다. visited[A, E, C]
    • C에서 갈 수 있는 노드들 중, 최단 경로를 갱신할 수 있는 노드를 확인한다.
    • C -> D(8) 이고, (C까지 가는 최소 비용 3) + (C -> D까지 가는 최소 비용 8)로 D 노드에 저장된 최소 비용과 비교한다.
    • D의 현재 최소 비용은 무한대이다. 11 < 무한대이기 때문에 D의 최소 비용을 11로 갱신한다.
    • D가 갱신될 때 직전 노드는 C이다. 직전 노드도 C로 갱신한다.
    • 후보 노드 A, E, C를 제외하고, 최소 비용이 제일 적은 B가 다음 후보 노드가 된다.
    • B를 후보 노드로 설정하고 visited에 B를 추가한다. visited[A, E, C, B]
    • B에서 갈 수 있는 노드들 중, 최단 경로를 갱신할 수 있는 노드를 확인한다.
    • B -> C(6) 이고, (B까지 가는 최소 비용 4) + (B -> C까지 가는 최소 비용 6)로 C 노드에 저장된 최소 비용과 비교한다.
    • C의 현재 최소 비용은 3이다. 10 > 3 이기 때문에 C의 최소 비용은 갱신하지 않는다.
    • 최소 비용이 갱신되지 않았으니 C의 직전 노드도 갱신하지 않는다.
    • 후보 노드 A, E, C, B를 제외하고 남은 D가 후보 노드가 된다.
    • D를 후보 노드로 설정하고 visited에 D를 추가한다. visited[A, E, C, B, D]
    • D에서 갈 수 있는 노드들 중, 최단 경로를 갱신할 수 있는 노드를 확인한다.
    • D -> A(5) 이고, (D까지 가는 최소 비용 11) + (D -> A까지 가는 최소 비용 5)로 A 노드에 저장된 최소 비용과 비교한다.
    • A의 현재 최소 비용은 0이다. 16 > 0 이기 때문에 A의 최소 비용은 갱신하지 않는다.
    • 최소 비용이 갱신되지 않았으니 A의 직전 노드도 갱신하지 않는다.
    • D -> B(2) 이고, (D까지 가는 최소 비용 11) + (D -> B까지 가는 최소 비용 2)로 B 노드에 저장된 최소 비용과 비교한다.
    • B의 현재 최소 비용은 4이다. 13 > 4 이기 때문에 B의 최소 비용은 갱신하지 않는다.
    • 최소 비용이 갱신되지 않았으니 B의 직전 노드도 갱신하지 않는다.
    • visited에 모든 노드가 담겼으니 더 이상 확인할 노드가 없다. 종료한다.
  • 다익스트라 알고리즘 결과 분석
    • C까지 가는 경로를 확인한다.
    • 최소 비용은 3이다.
    • C의 직전 노드는 E다. E로 이동한다.
    • E의 직전 노드는 A다. A로 이동한다.
    • A의 직전 노드는 A다. 종료한다.
    • A -> E -> C가 최소 비용 3으로 C로 가는 최단 경로임을 알 수 있다.
  • 다익스트라 알고리즘 구현하기
    • 후보 노드는 현재까지 후보 노드로 설정 되지 않았던 노드 중, 최소 비용이 가장 적은 노드
    • 최소 비용이 가장 적은 노드는 우선 순위 큐를 활용해서 확인한다.
    • 최소 비용이 갱신된 노드는 우선 순위 큐에 푸쉬
    • 우선 순위 큐에서 팝을 할 때 visited를 활용해 방문여부를 체크한다.
    • 방문했다면 아무 동작도 하지 않는다.
    • 방문하지 않았다면 최소 비용을 갱신한다.
    • 각 노드까지 최소 비용과 최단 경로가 업데이트 되어야 한다.
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

      class Dijkstra {
      private static final int INF = Integer.MAX_VALUE;
      // 전역 변수 선언
      private static List<List<Pair>> graph = new ArrayList<>(); // 그래프를 인접 리스트 형태로 저장
      private static int[] dist; // 각 노드까지의 최단 거리를 저장
      private static int[] prev; // 각 노드의 직전 노드를 저장
      private static boolean[] visited; // 방문 여부를 저장
                                                                  //
      // Pair 클래스를 정의하여 노드와 거리를 저장
      private static class Pair {
          int node;
          int distance;
          Pair(int node, int distance) {
              this.node = node;
              this.distance = distance;
          }
      }
                                                              //
      public static void dijkstra(int start) {
          int n = graph.size();        // 그래프의 노드 개수
          dist = new int[n];           // 최단 거리 배열
          prev = new int[n];           // 직전 노드 배열
          visited = new boolean[n];    // 방문 여부 배열
                                       //
          Arrays.fill(dist, INF);      // 최단 거리 배열을 무한대로 초기화
          Arrays.fill(prev, -1);       // 직전 노드 배열을 -1로 초기화
          dist[start] = 0;             // 시작 노드의 거리는 0으로 설정
                                       //
          // 최소 힙 (우선순위 큐)을 사용하여 최단 거리를 찾음
          PriorityQueue<Pair> pq = new PriorityQueue<>((o1, o2) -> Integer.compare(o1.distance, o2.distance));
          pq.offer(new Pair(start, 0)); // 시작 노드를 큐에 추가
                                        //
          // 큐가 빌 때까지 반복
          while (!pq.isEmpty()) {
              Pair pair = pq.poll();
              int u = pair.node;
                                                                     //
              // 현재 노드까지의 거리가 이미 더 짧은 경로가 있으면 무시
              if (visited[u]) continue;
              visited[u] = true;
                                                //
              // 현재 노드의 모든 인접 노드를 탐색
              for (Pair edge : graph.get(u)) {
                  int v = edge.node;         // 인접 노드
                  int weight = edge.distance; // 가중치
                                                       //
                  // 더 짧은 경로를 발견한 경우
                  if (dist[u] + weight < dist[v]) {
                      dist[v] = dist[u] + weight; // 최단 거리 업데이트
                      prev[v] = u;                // 직전 노드 업데이트
                      pq.offer(new Pair(v, dist[v])); // 큐에 추가
                  }
              }
          }
      }
                                            //
      // 경로를 출력하는 함수 (재귀 호출 사용)
      public static void printPath(int node) {
          if (node == -1) return;    // base case: 시작 노드에 도달
          printPath(prev[node]);     // 직전 노드로 재귀 호출
          System.out.print(node + " "); // 현재 노드 출력
      }
                                              //
      public static void main(String[] args) {
          // 그래프를 인접 리스트 형태로 정의
          // 각 Pair는 (인접 노드, 가중치)를 의미
          graph.add(Arrays.asList(new Pair(1, 4), new Pair(2, 4), new Pair(4, 1)));  // A (0)
          graph.add(new ArrayList<>());                                              // B (1)
          graph.add(Arrays.asList(new Pair(1, 6), new Pair(3, 8)));                  // C (2)
          graph.add(Arrays.asList(new Pair(1, 2)));                                  // D (3)
          graph.add(Arrays.asList(new Pair(2, 2)));                                  // E (4)
                                                      //
          int start = 0; // 시작 노드 (A)
          dijkstra(start); // 다익스트라 알고리즘 실행
                                                          //
          // 결과 출력
          System.out.println("Node\tDistance\tPath");
          for (int i = 0; i < dist.length; ++i) {
              System.out.print(i + "\t" + dist[i] + "\t\t");
              printPath(i);
              System.out.println();
          }
      }
  }

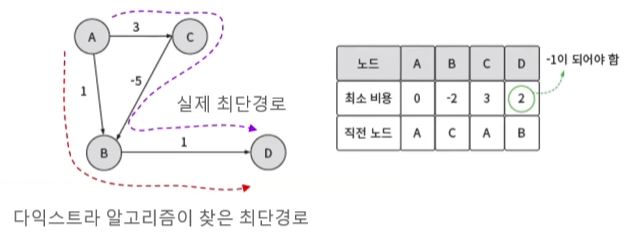
음의 가중치가 있는 그래프에서 다익스트라 알고리즘

  • algorithm-study
    • A -> B 보다 A -> C -> B 경로가 비용이 더 적다.
    • 하지만 A -> B가 1이고 A -> C가 3이라 A -> B를 찾는다.
    • 이런 이유로 음의 가중치가 있을 경우 다익스트라의 정상 동작을 보장할 수 없다.
    • 음의 가중치가 있을 경우 밸만-포드 알고리즘을 사용해야 한다.

전력망을 둘로 나누기 문제 풀이

  • 전력망을 둘로 나누기
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

      import java.util.*;
                                                  //
  class Solution {
      private static boolean[] visited;
      private static List<Integer>[] adj;
      private static int N, answer;
                                                  //
      public int solution(int n, int[][] wires) {
          N = n;
          answer = n - 1;
                                                  //
          adj = new ArrayList[n + 1];
          for (int i = 1; i <= n; i++) {
              adj[i] = new ArrayList<>();
          }
                                               //
          for (int[] wire : wires) {
              adj[wire[0]].add(wire[1]);
              adj[wire[1]].add(wire[0]);
          }
                                              //
          visited = new boolean[n + 1];
                                              //
          dfs(1);
                                              //
          return answer;
      }
                                              //
      private static int dfs(int now) {
          visited[now] = true;
                                              //
          int sum = 0;
                                              //
          for (int next : adj[now]) {
              if (!visited[next]) {
                  int cnt = dfs(next);
                                                                      //
                  answer = Math.min(answer, Math.abs(N - cnt * 2));
                                                                      //
                  sum += cnt;
              }
          }
                                                                      //
          return sum + 1;
      }
  }
  • 못 풀었다. ㅠㅠ ↑ 풀이 ↑
  • dfs의 answer와 sum을 구하는 방법이 이해가 되질 않는다. 계속 풀어보고 복습해야겠다.

양과 늑대 문제 풀이

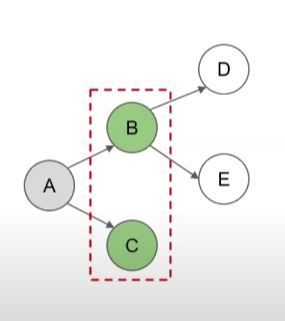
  • 양과 늑대
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

      class Solution {
      int answer = 0;
      boolean[] checked;
                                                                  //
      public int solution(int[] info, int[][] edges) {
          checked = new boolean[(int) Math.pow(2, info.length)];
          dfs(0, new boolean[info.length], 0, 0, info, edges, 1);
          return answer;
      }
                                                                                                                      //
      private void dfs(int idx, boolean[] visited, int sheep, int wolf, int[] info, int[][] edges, int state) {
          visited[idx] = true;
          checked[state] = true;
                                                                                                                      //
          if(info[idx] == 0) {
              sheep++;
              answer = Math.max(sheep, answer);
          } else {
              wolf++;
          }
                                                                                                                      //
          if(sheep <= wolf) {
              return;
          }
                                                                                                                      //
          for (int[] edge : edges) {
              if(visited[edge[0]] && !visited[edge[1]] && !checked[state | (1<<edge[1])]) {
                  boolean[] newVisited = visited.clone();
                  dfs(edge[1], newVisited, sheep, wolf, info, edges, state | (1<<edge[1]));
              }
          }
      }
  }
  • 못 풀었다. ㅠㅠ ↑ 풀이 ↑
  • 1시간을 보고 문제에 손도 못대고 숨이 턱 막혔고, 다른 사람의 풀이를 보고 벽을 느꼈다.
  • 계속해서 풀어봐야겠다… 쉽지 않다..

미로 탈출 문제 풀이

  • 미로 탈출
  • 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

      import java.util.*;
                                                              //
  class Solution {
                                                              //
      private static final int[] dx = {0, 0, -1, 1};
      private static final int[] dy = {-1, 1, 0, 0};
                                                              //
      private static class Point {
          int nx, ny;
                                                              //
          public Point(int nx, int ny) {
              this.nx = nx;
              this.ny = ny;
          }
      }
                                                              //
      private static char[][] map;
      private static int N, M;
                                                              //
      public int solution(String[] maps) {
          N = maps.length;
          M = maps[0].length();
                                                              //
          map = new char[N][M];
          for (int i = 0; i < N; i++) {
              map[i] = maps[i].toCharArray();
          }
                                                              //
          Point start = null, end = null, lever = null;
                                                              //
          for (int i = 0; i < N; i++) {
              for (int j = 0; j < M; j++) {
                  if (map[i][j] == 'S') start = new Point(j, i);
                  else if (map[i][j] == 'E') end = new Point(j, i);
                  else if (map[i][j] == 'L') lever = new Point(j, i);
              }
          }
                                                                          //
          int startLever = bfs(start, lever);
          int leverEnd = bfs(lever, end);
                                                                          //
          if (startLever == -1 || leverEnd == -1) {
              return -1;
          } else {
              return startLever + leverEnd;
          }
      }
                                                                          //
      private static int bfs(Point start, Point end) {
          int[][] dist = new int[N][M];
          ArrayDeque<Point> queue = new ArrayDeque<>();
          dist[start.ny][start.nx] = 1;
          queue.add(start);
                                                                          //
          while (!queue.isEmpty()) {
              Point now = queue.poll();
              for (int i = 0; i < 4; i++) {
                  int nextX = now.nx + dx[i];
                  int nextY = now.ny + dy[i];
                                                                          //
                  if (nextX < 0 || nextX >= M || nextY < 0 || nextY >= N) {
                      continue;
                  }
                                                                          //
                  if (dist[nextY][nextX] > 0) {
                      continue;
                  }
                                                                          //
                  if (map[nextY][nextX] == 'X') {
                      continue;
                  }
                                                                          //
                  dist[nextY][nextX] = dist[now.ny][now.nx] + 1;
                                                                          //
                  queue.add(new Point(nextX, nextY));
                                                                          //
                  if (nextX  == end.nx && nextY == end.ny) {
                      return dist[end.ny][end.nx] - 1;
                  }
              }
          }
          return -1;
      }
  }
  • 못 풀었다. ㅠㅠ ↑ 풀이 ↑
  • 그래프가 너무 어렵다 ㅠㅠ 한 문제도 못 풀었다… 심각한 듯 하다.
  • 개념을 보고 익숙해질 때 까지 반복 숙달을 해야겠다 ㅠㅠ
Algorithm, Study
java algorithm study