[코딩테스트 합격자 되기 스터디] 4주차 - 트리 (7.28 ~ 8.3)

---

코딩테스트 합격자 되기 스터디 4주차

강의 보기 -> 해당되는 부분 책 다시 읽기 -> 블로그 정리
강의는 C++로 되어 있지만 개념적인 내용이라 언어 상관 없이 보고 코드는 각 언어에 맞게 바꾸면 된다.

참고 강의 및 책

인프런 : 코딩테스트 합격자 되기 파이썬, C+_+ 저자님 인프런 강의 링크
Youtube : 코딩테스트 합격자 되기 파이썬, C+_+ 저자님 Youtube 링크
종이책 : 코딩테스트 합격자 되기 파이썬 편
종이책 : 코딩테스트 합격자 되기 C++ 편
종이책 : 코딩테스트 합격자 되기 자바스크립트 편
종이책 : 코딩테스트 합격자 되기 자바 편

트리

• 노드와 간선으로 이루어진 계층적 자료구조(부모-자식 관계 존재)
  • 계층적 자료구조 : 위, 아래 개념이 있다. (ex) - 회사 직급 (사장 - 부사장 - 팀장)
• 순환을 허용하지 않음
  
• 코딩 테스트에서는 이진트리(자식 노드가 최대 2개인 트리)만 알면 된다.
  

트리의 용어

• 루트 노드 : 최상위에 있는 노드, 트리에서 유일하다.
  
• 자식 노드 : 노드 아래에 연결된 다른 노드가 있으면 부모-자식 관계이고 아래에 있는 노드가 자식 노드다.
  
• 형제 노드 : 부모-자식 관계 노드에서 자식 노드가 2개 이상 있으면 자식 노드는 서로 형제노드다.
  
• 리프 노드 : 자식 노드가 없을 경우 리프 노드라고 한다.
  
• 차수 : 루트 노드의 자식 노드 개수를 말한다. 루트 노드의 자식 노드가 3개면 루트 노드의 차수는 3이다.
  
• 레벨 : 루트 노드는 레벨 0, 자식 노드로 내려갈 때 마다 1레벨씩 올라간다.
  • 자식 노드와 루트 노드 사이에 몇 개의 간선이 있는 지를 나타낸다.
• 높이 : 루트 노트에서 가장 깊이 들어갈 수 있는 노드를 말한다. 즉, 가장 높은 레벨이 높이다.
  

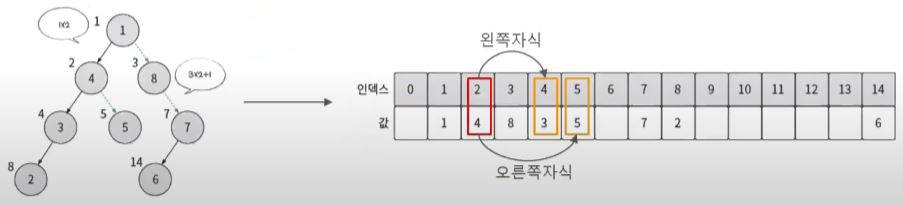
이진 트리 표현 하기 - 배열

• 루트 노드 인덱스는 1, 0으로 해도 되지만 1로 했을 때에 비해 크게 효율적이지 못하다.
  
• 왼쪽 자식 노드의 인덱스는 부모 노드 인덱스 * 2
  
• 오른쪽 자식 노드의 인덱스는 부모 노드 인덱스 * 2 + 1
  
• 인덱스 공식만 활용하므로 구현 난이도가 낮다.
  
• 메모리 공간을 낭비할 수 있는 문제점이 있다. 아래 사진에 사용하지 않는 공간이 많다.
  
• 
  

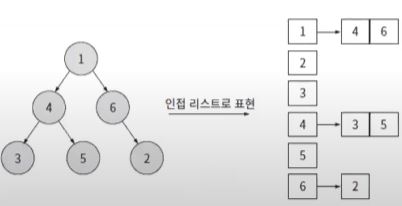
이진 트리 표현 하기 - 인접 리스트

• 각 리스트의 인덱스는 부모 노드
  
• 자식 노드는 부모 노드에 해당되는 인덱스에 추가
  
• 배열 보다 공간 효율이 좋다.
  
• 자식 노드를 찾는데 오래 걸릴 수 있다.
  • 순차탐색 필요, 이진 트리는 자식이 2개라 크게 단점이 없다.
• 
  

이진 트리의 순회

• 순회 : 트리의 노드를 모두 방문하는 방법
  
• 현재 노드를 언제 방문 하는지에 따라 전위 순회, 중위 순회, 후위 순회로 분류된다.
  

이진 트리의 순회 - 전위 순회

• 부모 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드 순으로 방문한다.
  
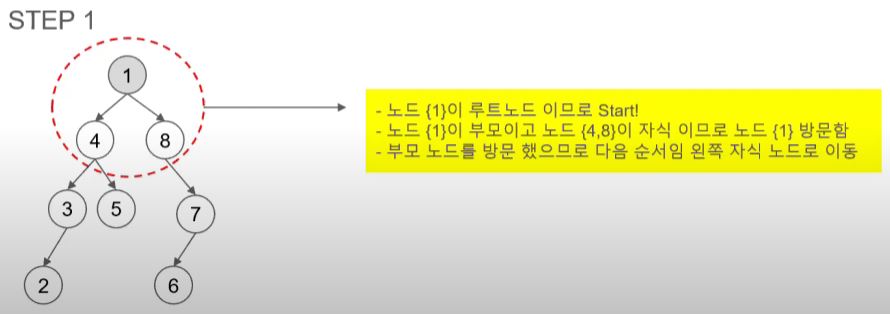
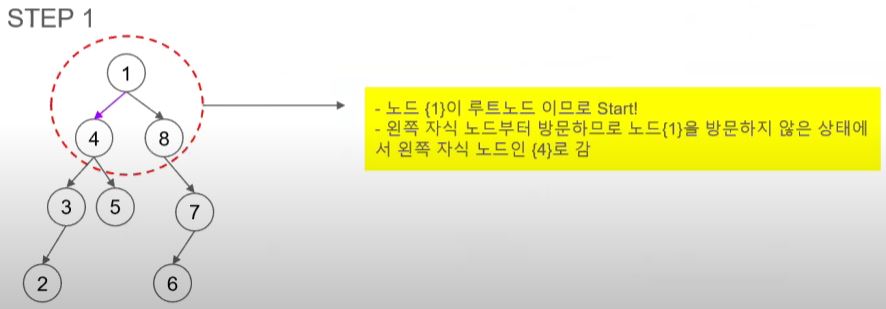
• 루트노드 부터 시작
  
• 
  • 1이 루트 노드라 1부터 시작한다.
  • 1은 부모 노드이니 방문한다.
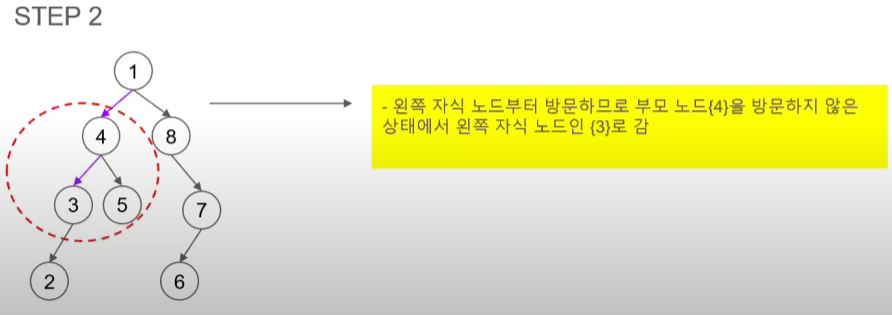
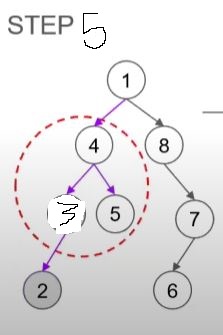
  • 1의 자식 노드 중 왼 쪽인 4를 방문한다.
• 
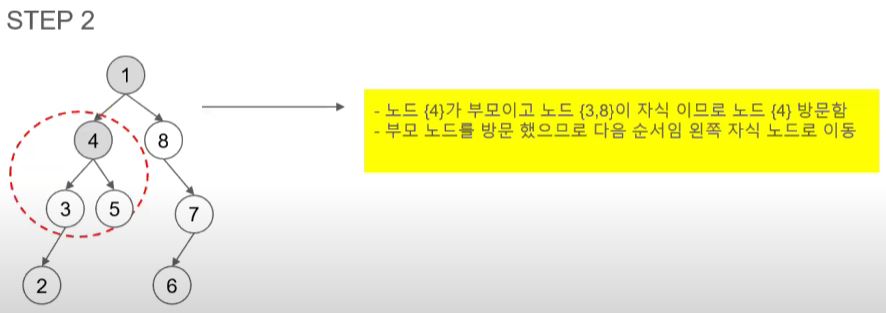
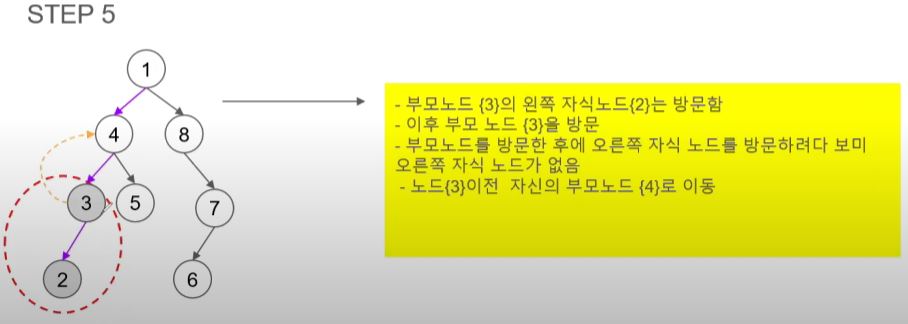
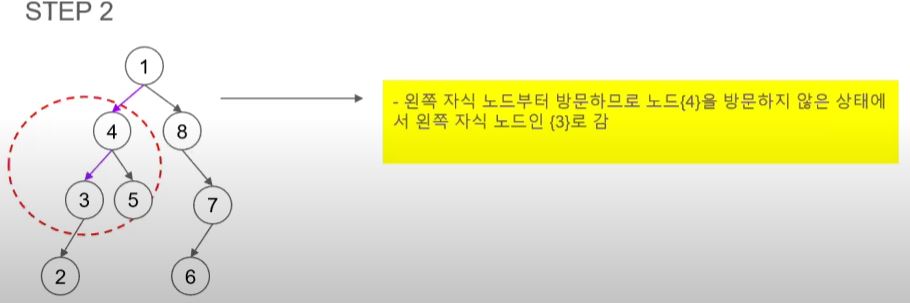
  • 다음은 오른쪽 자식 노드를 방문해야 하지만 4는 자식이 있어 부모 노드가 된다.
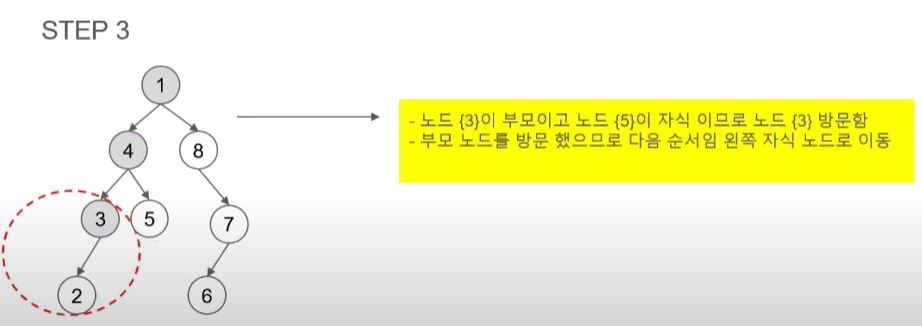
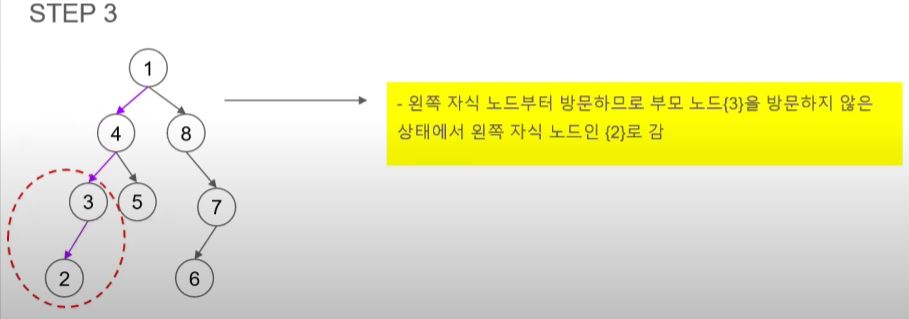
  • 4의 왼쪽 자식 노드인 3을 방문한다.
• 
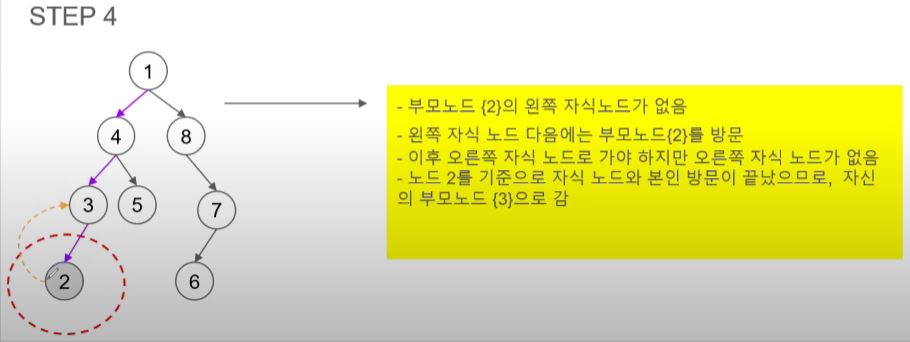
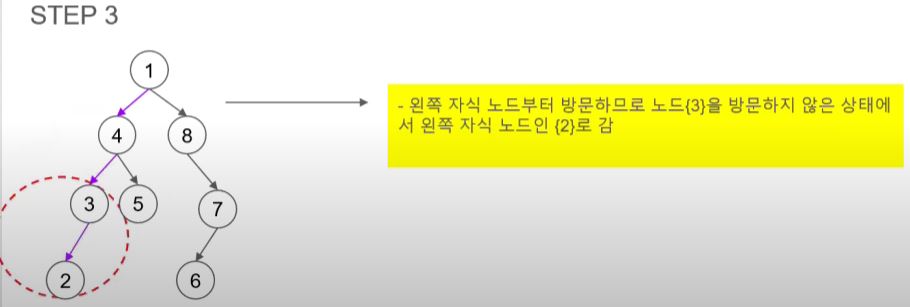
  • 여기서도 오른쪽 노드를 방문해야 하지만 3이 부모 노드라 자식인 2를 방문한다.
• 
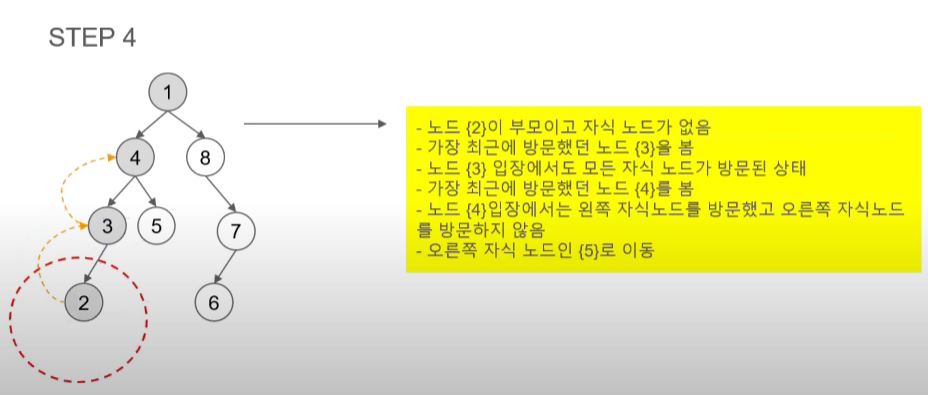
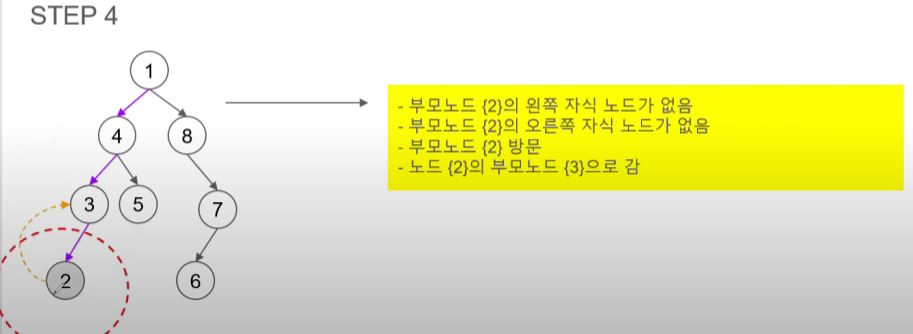
  • 2는 부모 노드지만 자식이 없어 가장 최근에 방문한 곳으로 돌아간다.
  • 3은 이미 방문을 했고 오른쪽 자식 노드가 없어 3을 방문하기 전인 4로 돌아간다.
• 
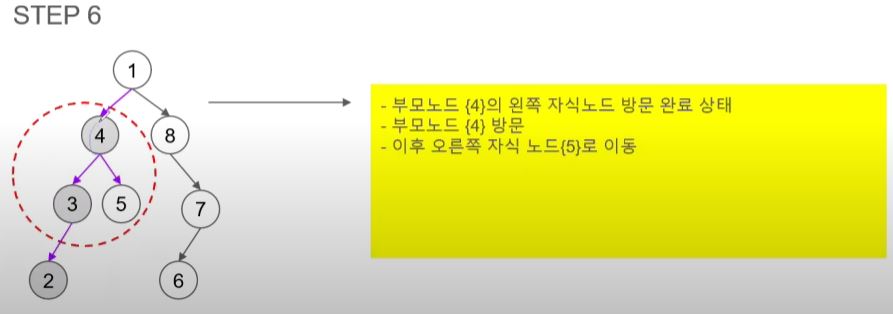
  • 4에는 오른쪽 자식 노드가 있어 5를 방문한다.
  • 5에는 자식 노드가 없어 최근에 방문한 곳으로 돌아간다.
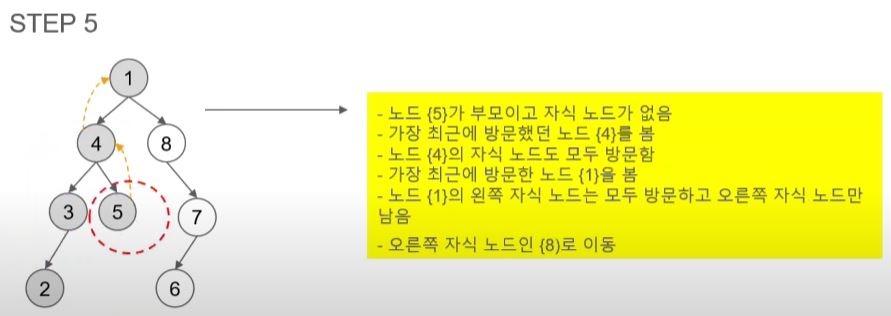
  • 4는 모든 노드를 방문했기 때문에 4를 방문하기 전인 1로 돌아간다.
• 
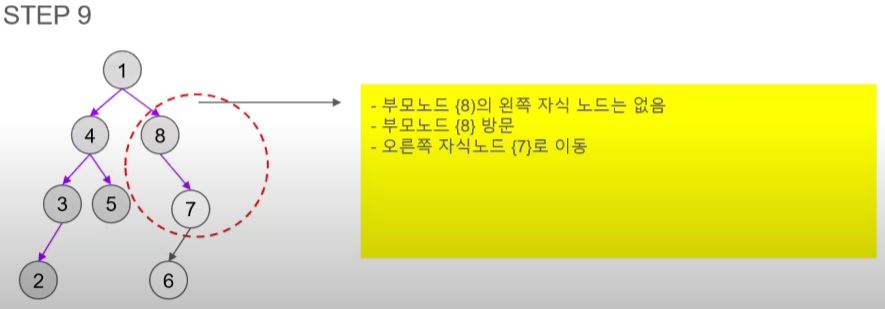
  • 1에는 오른쪽 자식 노드가 있어 8을 방문한다.
• 
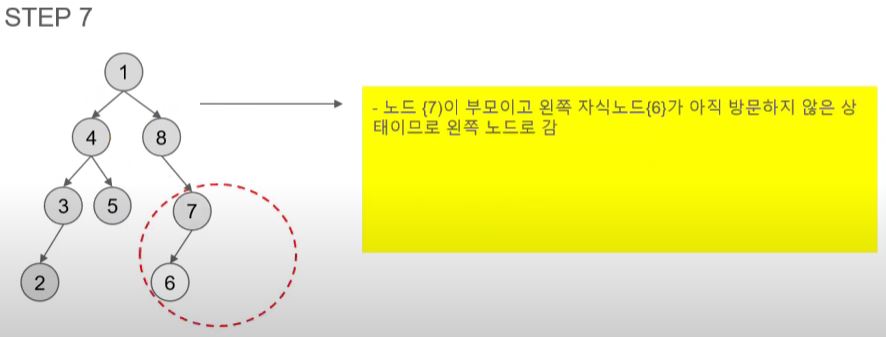
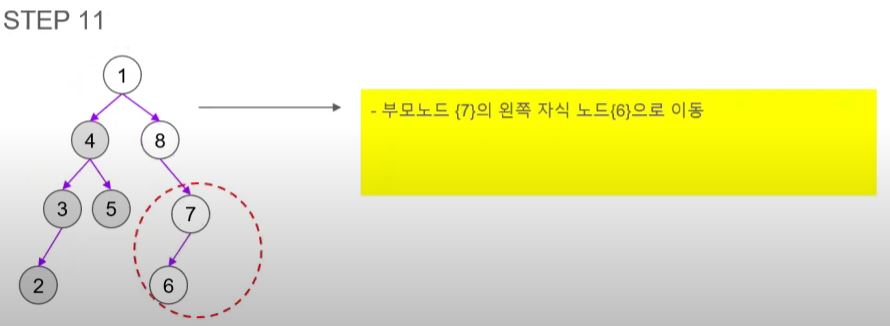
  • 8에는 왼쪽 자식 노드가 없으니 오른쪽 자식 노드인 7을 방문한다.
• 
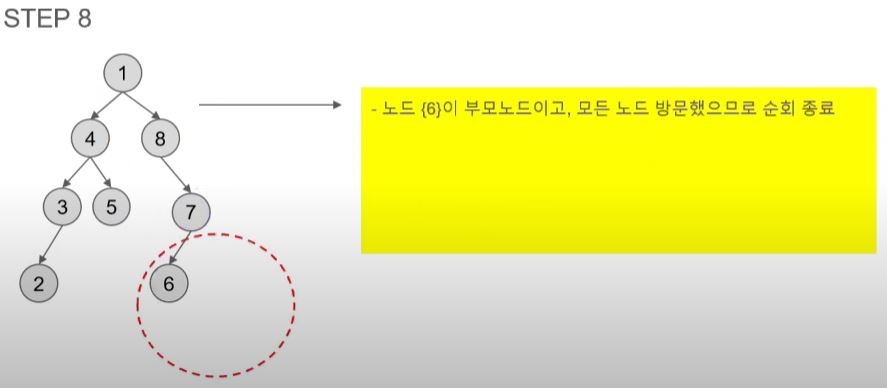
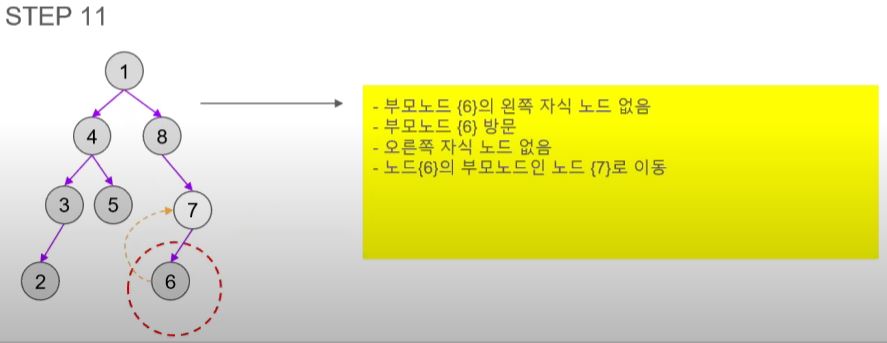
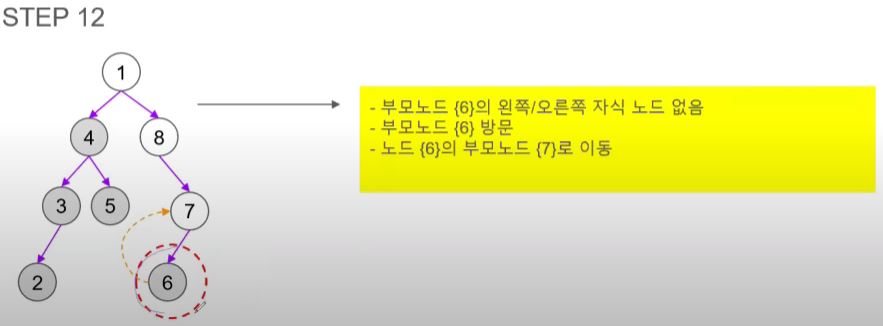
  • 7의 왼쪽 자식 노드인 6을 방문한다.
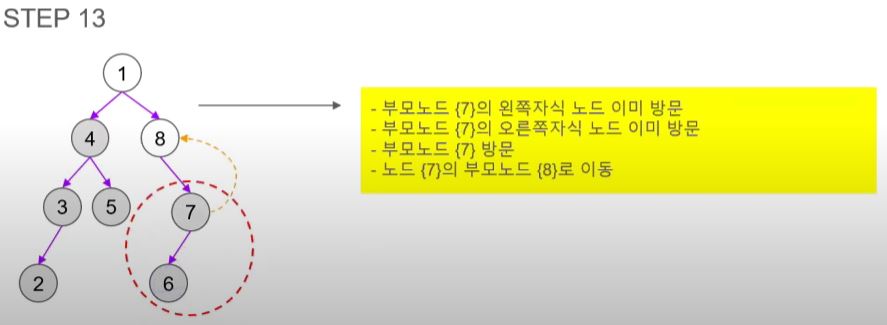
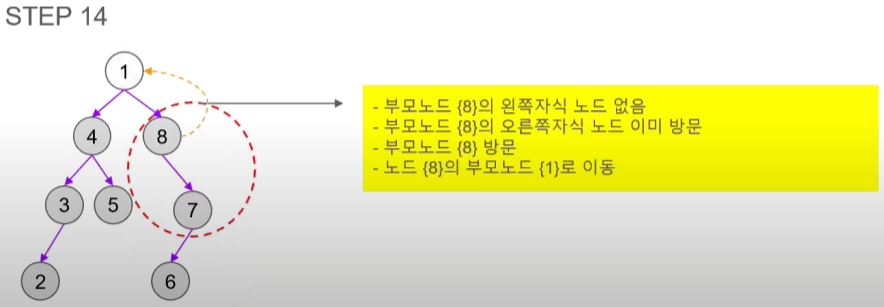
  • 모든 노드를 방문했으니 순회를 종료한다.

    public static void main(String[] args) {
      // 트리를 배열로 나타내기
      // -1은 해당 위치에 노드가 없음을 나타냅니다.
      int[] tree = {-1, 1, 4, 8, 3, 5, -1, 7, 2, -1, -1, -1, -1, -1, 6};
      int size = tree.length;
      preorderTraversal(tree, 1, size); // 전위 순회 함수 호출
    }
    public static void preorderTraversal(int[] tree, int index, int size) {
      if (index >= size || tree[index] == -1) {
      return; // 유효하지 않은 인덱스나 값이 -1이면 종료
      }
      System.out.print(tree[index] + " "); // Step 1: 현재 노드 값 출력
      preorderTraversal(tree, 2 * index, size); // Step 2: 왼쪽 자식 노드로 이동 (2*index)
      preorderTraversal(tree, 2 * index + 1, size); // Step 3: 오른쪽 자식 노드로 이동 (2*index + 1)
    }
    

• 트리를 복사할 때 사용한다.
  • 루트 노드부터 트리 노드를 순차적으로 복사할 수 있음
• 코드 및 이미지는 코딩테스트 합격자 되기 파이썬, C+_+ 저자님 Youtube 링크에서 참고했다.
  
• dfs 문제와 유사하게 재귀 함수를 사용한다.
  

이진 트리의 순회 - 중위 순회

• 왼쪽 자식 노드 -> 부모 노드 -> 오른쪽 자식 노드 순으로 방문한다.
  
• 루트노드 부터 시작
  
• 
  • 1이 루트 노드이니 1부터 시작한다.
  • 왼쪽 자식 노드부터 방문하니 1의 왼쪽 자식 노드인 4로 이동한다.
• 
  • 4를 방문 해야 하지만 4에는 또 왼쪽 자식 노드인 3이 있다. 3으로 이동한다.
• 
  • 3을 방문 해야 하지만 3에는 왼쪽 자식 노드인 2가 있다. 2로 이동한다.
• 
  • 2로 이동이 된 순간 2는 부모 노드가 되었다.
  • 2는 왼쪽 자식 노드가 없으니 부모 노드인 2를 방문한다.
• 
  • 2의 오른쪽 자식 노드가 없으니 부모 노드인 3으로 돌아간다.
  • 3의 왼쪽 자식 노드는 이미 방문을 했으니 부모 노드인 3을 방문한다.
• 
  • 3의 오른쪽 자식 노드가 없으니 부모 노드인 4로 돌아간다.
  • 4의 왼쪽 자식 노드는 이미 방문을 했으니 부모 노드인 4를 방문한다.
• 
  • 4의 오른쪽 자식 노드인 5로 이동한다.
  • 5의 왼쪽 자식 노드가 없으니 부모 노드인 5를 방문한다.
• 
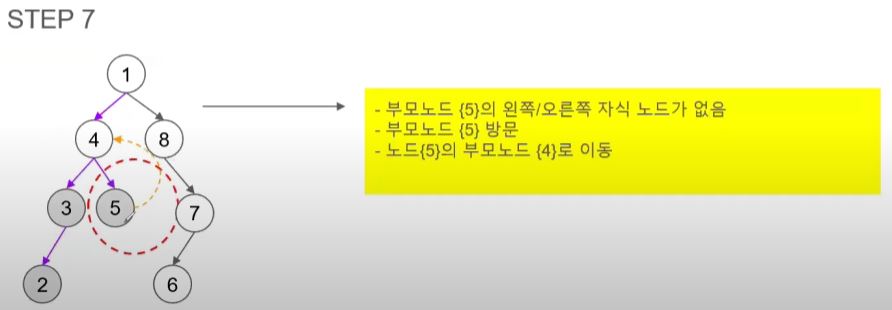
  • 5의 오른쪽 자식 노드가 없으니 부모 노드인 4로 돌아간다.
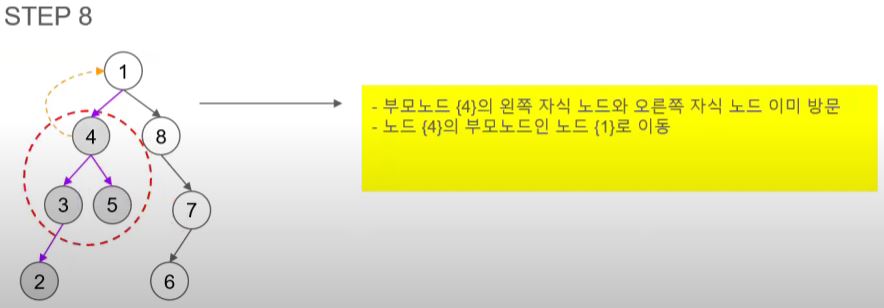
  • 부모 노드인 4와 자식 노드를 모두 방문 했으니 4의 부모 노드인 1로 돌아간다.
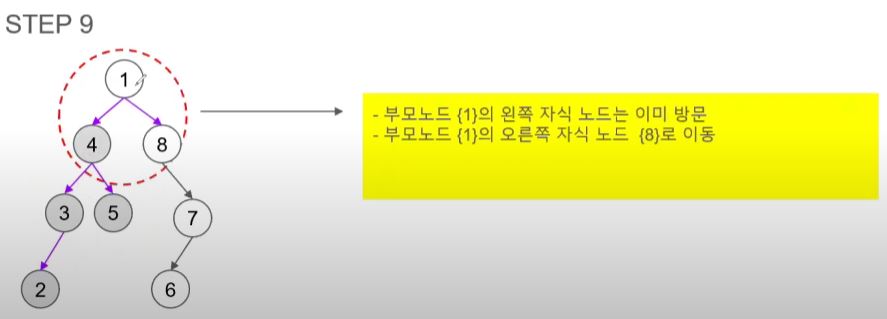
  • 1의 왼쪽 자식 노드인 4는 이미 방문 했으니 부모 노드인 1을 방문한다.
• 
  • 1의 오른쪽 자식 노드인 8로 이동한다.
  • 8의 왼쪽 자식 노드가 없으니 부모 노드인 8을 방문한다.
• 
  • 8의 오른쪽 자식 노드인 7로 이동한다.
  • 7의 왼쪽 자식 노드인 6으로 이동한다.
• 
  • 6의 왼쪽 자식 노드가 없으니 부모 노드인 6을 방문한다.
• 
  • 6의 오른쪽 자식 노드가 없으니 부모 노드인 7로 돌아간다.
  • 7의 왼쪽 자식 노드인 6은 이미 방문 했으니 부모 노드인 7을 방문한다.
  • 7의 오른쪽 자식 노드는 없고 순회가 끝났으니 순회를 종료한다.
• 이진 탐색 트리의 원소를 정렬된 상태로 순회한다.
  • 왼쪽은 부모보다 작다. 아래 사진의 1번
  • 오른쪽은 부모보다 크다. 아래 사진의 3번
• 
  • 방문 순서 : 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7

    public static void main(String[] args) {
      // 트리를 배열로 나타내기
      // -1은 해당 위치에 노드가 없음을 나타냅니다.
      int[] tree = {-1, 1, 4, 8, 3, 5, -1, 7, 2, -1, -1, -1, -1, -1, 6};
      int size = tree.length;
      inorderTraversal(tree, 1, size); // 중위 순회 함수 호출
    }
    public static void inorderTraversal(int[] tree, int index, int size) {
      if (index >= size || tree[index] == -1) {
      return; // 유효하지 않은 인덱스나 값이 -1이면 종료
      }
      inorderTraversal(tree, 2 * index, size); // Step 1: 왼쪽 자식 노드로 이동 (2*index)
      System.out.print(tree[index] + " "); // Step 2: 현재 노드 값 출력
      inorderTraversal(tree, 2 * index + 1, size); // Step 3: 오른쪽 자식 노드로 이동 (2*index + 1)
    }
    

이진 트리의 순회 - 후위 순회

• 왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 부모 노드 순으로 방문한다.
  
• 루트 노드부터 시작
  
• 
  • 1이 루트 노드이니 1부터 시작한다.
  • 왼쪽 자식 노드 부터 방문하니 1의 왼쪽 자식 노드인 4로 이동한다.
• 
  • 4를 방문해야 하지만 왼쪽 자식 노드인 3이 있어 3으로 이동한다.
• 
  • 3을 방문해야 하지만 왼쪽 자식 노드인 2가 있어 2로 이동한다.
• 
  • 2의 왼쪽 자식 노드, 오른쪽 자식 노드가 없으니 부모 노드인 2를 방문한다.
• 
  • 2의 방문이 끝났으니 부모 노드인 3으로 돌아간다.
  • 3의 왼쪽 자식 노드인 2는 방문 했고, 오른쪽 자식 노드는 없으니 부모 노드인 3을 방문한다.
• 
  • 왼쪽 자식 노드인 3의 방문이 끝났으니 오른쪽 자식 노드인 5로 이동한다.
• 
  • 5의 왼쪽 자식 노드, 오른쪽 자식 노드가 없으니 부모 노드인 5를 방문한다.
• 
  • 5의 방문이 끝났으니 부모 노드인 4로 돌아간다.
  • 4의 왼쪽 자식 노드, 오른쪽 자식 노드를 모두 방문 했으니 부모 노드인 4를 방문한다.
• 
  • 4의 방문이 끝났으니 부모 노드인 1로 돌아간다.
  • 왼쪽 자식 노드인 4의 방문이 끝났으니 오른쪽 자식 노드인 8로 이동한다.
• 
  • 8의 왼쪽 자식 노드가 없으니 오른쪽 자식 노드인 7로 이동한다.
• 
  • 7의 왼쪽 자식 노드인 6으로 이동한다.
• 
  • 6의 왼쪽 자식 노드, 오른쪽 자식 노드가 없으니 부모 노드인 6을 방문한다.
• 
  • 6의 방문이 끝났으니 부모 노드인 7로 돌아간다.
  • 7의 왼쪽 자식 노드인 6의 방문 했고, 오른쪽 자식 노드는 없으니 부모 노드인 7을 방문한다.
• 
  • 7의 방문이 끝났으니 부모 노드인 8로 돌아간다.
  • 8의 오른쪽 자식 노드 방문이 끝났으니 부모 노드인 8을 방문한다.
• 
  • 오른쪽 자식 노드인 8의 방문이 끝났으니 부모 노드인 1을 방문한다.
  • 모든 노드의 순회가 완료 되었으니 순회를 종료한다.
• 폴더 삭제 하기
  • 제일 깊숙이 들어있는 폴더부터 삭제해야 한다.
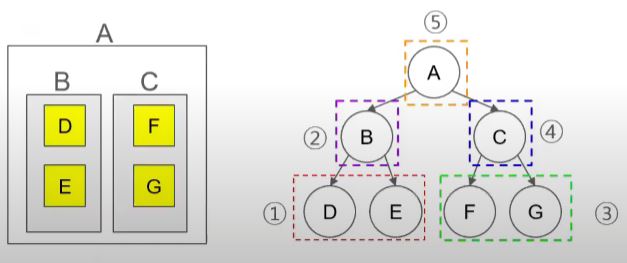
  • 아래 사진의 숫자 순서대로 삭제한다. 1 -> 2 -> 3 -> 4 -> 5 순으로 삭제
  • 트리 삭제를 할 때 후위 순회를 사용하면 된다.
• 
  

  public static void main(String[] args) {
    // 트리를 배열로 나타내기
    // -1은 해당 위치에 노드가 없음을 나타냅니다.
    int[] tree = {-1, 1, 4, 8, 3, 5, -1, 7, 2, -1, -1, -1, -1, -1, 6};
    int size = tree.length;
    inorderTraversal(tree, 1, size); // 후위 순회 함수 호출
  }
  public static void inorderTraversal(int[] tree, int index, int size) {
    if (index >= size || tree[index] == -1) {
        return; // 유효하지 않은 인덱스나 값이 -1이면 종료
    }
    inorderTraversal(tree, 2 * index, size); // Step 1: 왼쪽 자식 노드로 이동 (2*index)
    inorderTraversal(tree, 2 * index + 1, size); // Step 2: 오른쪽 자식 노드로 이동 (2*index + 1)
    System.out.print(tree[index] + " "); // Step 3: 현재 노드 값 출력
  }
  

이진 트리 탐색

• 탐색을 효율적으로 하기 위해 만든 이진 트리
• 왼쪽 자식 노드는 부모 노드보다 작은 값
• 오른쪽 자식 노드는 부모 노드보다 큰 값

이진 트리 탐색 삽입

• 
  • 3 삽입
  • 4 삽입, 3보다 크니 3의 오른쪽 자식 노드에 삽입
  • 2 삽입, 3보다 작으니 3의 왼쪽 자식 노드에 삽입
  • 8 삽입, 4보다 크니 4의 오른쪽 자식 노드에 삽입
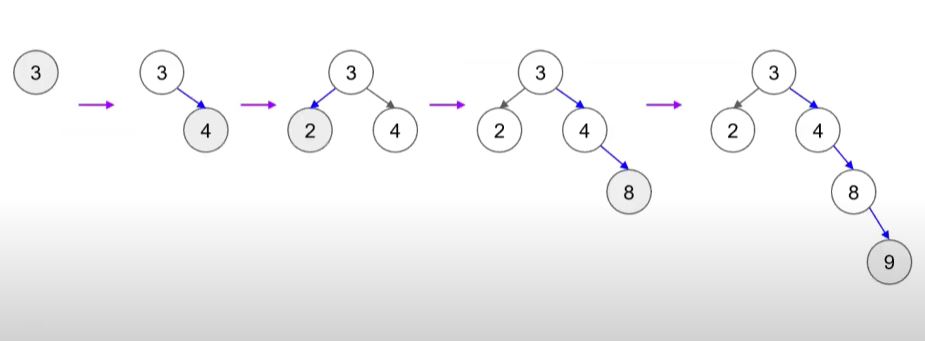
  • 9 삽입, 8보다 크니 8의 오른쪽 자식 노드에 삽입

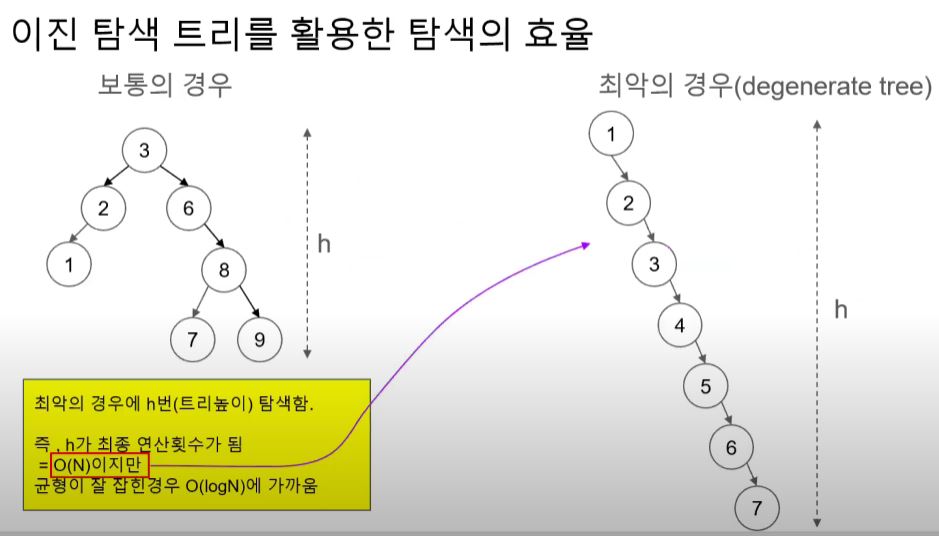
이진 트리 탐색를 활용한 탐색의 효율

• 
  • 원소가 삽입될 때 마다 정렬 되어야 하는 경우에 일반 정렬을 매 번 하는 것 보다 빠른 구조를 가진다.

이진 트리 탐색 특성

• 최대 탐색 횟수는 트리의 높이와 같다.
  • 최악의 경우 : O(N)
  • 균형 유지시 : O(logN)
• 삽입과 동시에 정렬을 한다.
  • 최악의 경우 : O(N)
  • 균형 유지시 : O(logN)
• map, set의 내부는 균형 이진 탐색 트리로 되어있음
  • 자바의 경우 TreeMap, TreeSet은 균형 이진 탐색 트리 (키 값 기준으로 정렬한다.)
  • HashMap, HashSet은 해시 테이블을 사용한다. (키 값 기준으로 정렬되지 않는다.)

길 찾기 게임 문제 풀이

• 길 찾기 게임
  

  static class Node {
    int id;
    int x;
    int y;
    Node left;
    Node right;
    Node(int id, int x, int y) {
        this.id = id;
        this.x = x;
        this.y = y;
    }
  }
  public int[][] solution(int[][] nodeinfo) {
    int n = nodeinfo.length;
    List<Node> nodes = new ArrayList<>();
    for (int i = 0; i < n; i++) {
        nodes.add(new Node(i + 1, nodeinfo[i][0], nodeinfo[i][1]));
    }
    nodes.sort((a, b) -> {
        if (a.y == b.y) {
            return a.x - b.x;
        } else {
            return b.y - a.y;
        }
    });
    Node root = buildTree(nodes);
    List<Integer> preorderList = new ArrayList<>();
    List<Integer> postorderList = new ArrayList<>();
    preorderTraversal(root, preorderList);
    postorderTraversal(root, postorderList);
    int[][] answer = new int[2][n];
    for (int i = 0; i < n; i++) {
        answer[0][i] = preorderList.get(i);
        answer[1][i] = postorderList.get(i);
    }
    return answer;
  }
  private Node buildTree(List<Node> nodes) {
    if (nodes.isEmpty()) return null;
    Node root = nodes.get(0);
    List<Node> leftSubtree = new ArrayList<>();
    List<Node> rightSubtree = new ArrayList<>();
    for (int i = 1; i < nodes.size(); i++) {
        Node node = nodes.get(i);
        if (node.x < root.x) {
            leftSubtree.add(node);
        } else {
            rightSubtree.add(node);
        }
    }
    root.left = buildTree(leftSubtree);
    root.right = buildTree(rightSubtree);
    return root;
  }
  private void preorderTraversal(Node node, List<Integer> list) {
    if (node == null) return;
    list.add(node.id);
    preorderTraversal(node.left, list);
    preorderTraversal(node.right, list);
  }
  private void postorderTraversal(Node node, List<Integer> list) {
    if (node == null) return;
    postorderTraversal(node.left, list);
    postorderTraversal(node.right, list);
    list.add(node.id);
  }
  

• 못 풀었다..ㅠㅠ 시간이 좀 지나고 다시 풀어보도록 해야겠다. ↑ 풀이 ↑
  

예상 대진표 문제 풀이

• 예상 대진표
  

  public int solution(int n, int a, int b)
  {
    int answer = 0;
    while (a != b) {
        a = (a + 1) / 2;
        b = (b + 1) / 2;
        answer++;
    }
    return answer;
  }
  

• 1라운드에서 만날 때, 다른 조일 때, 같은 조일 때를 나눠서 풀었는데 안풀렸다.
  
• 차분히 문제를 파악하고 시간 복잡도를 생각하면서 문제를 풀어야겠다.